Mseemab wrote:Hi there everyone,
Can anyone help with the below question please? I don't get how the second equation is sufficient.. :/

A tank is filled with gasoline to a depth of exactly 2 feet. The tank is a cylinder resting horizontally on its side, with its circular ends oriented vertically. The inside of the tank is exactly 6 feet long. What is the volume of gasoline in the tank?

(2) The top surface of the gasoline forms a rectangle that has an area of 24 square feet.

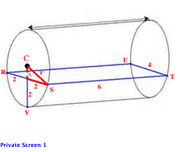
In the figure above, C is the center of the left circular base and rectangle RSTU is the surface of water.
Since the area of RSTU = 24, and it is given that ST=6, RS=4.
Since C is the center of the circular base, CV is a radius that bisects RS into two lengths of 2.

CV:
The figure indicates that CV is equal to the sum of x and and the height of the water (2).
Since CV is a radius, we get:
r = x+2
x = r-2.

Red triangle:
In the red triangle, x and 2 are legs and CS is both the hypotenuse of the triangle and the radius of the cylinder.
Thus:
x² + 2² = r².

Substituting x=r-2 into x² + 2² = r², we get:
(r-2)² + 2² = r²
r² - 4r + 4 + 4 = r²
8 = 4r
r = 2.

Thus, the height of the water -- 2 -- is equal to the radius of the cylinder.
Since the height of the water is equal to HALF the diameter, the volume of the water is equal to HALF the volume of the cylinder.
Since we can calculate the volume of the cylinder using r=2 and h=6, the volume of the water can be determined.
SUFFICIENT.

Mseemab wrote:Hi there everyone,
Can anyone help with the below question please? I don't get how the second equation is sufficient.. :/

A tank is filled with gasoline to a depth of exactly 2 feet. The tank is a cylinder resting horizontally on its side, with its circular ends oriented vertically. The inside of the tank is exactly 6 feet long. What is the volume of gasoline in the tank?

(2) The top surface of the gasoline forms a rectangle that has an area of 24 square feet.

An alternate approach:

RULE:
If points A, B and C are not collinear and are all the same distance from point O, then points A, B and C lie on a unique circle with center O.



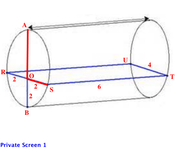
In the figure above, AB is the diameter of the left circular base and rectangle RSTU is the surface of water.
Since the area of RSTU = 24, and it is given that ST=6, RS=4.
Since AB is the diameter of the circular base, AB bisects RS into two lengths of 2.

Since points R, S and B are all equidistant from point O, points R, S and B lie on a unique circle with center O.
Implication:
O is the center of the left circular base, on which lie points R, S and B.

Thus, the height of the water -- 2 -- is equal to the radius of the cylinder.
Since the height of the water is equal to HALF the diameter, the volume of the water is equal to HALF the volume of the cylinder.
Since we can calculate the volume of the cylinder using r=2 and h=6, the volume of the water can be determined.
SUFFICIENT.