In triangle ABC, point Xis the midpoint of sideAC and
point Yis the midpoint of side BC. If point Ris the
midpoint of line segment XC and if point S is the
midpoint of line segment YC, what is the area of
triangular region RCS1
(1) The area of triangular region ABX is 32.
(2) The length of one of the altitudes of triangle ABC
is 8
Need to understand the logic please
This topic has expert replies
-
[email protected]
- Master | Next Rank: 500 Posts
- Posts: 429
- Joined: Wed Sep 19, 2012 11:38 pm
- Thanked: 6 times
- Followed by:4 members
-
Matt@VeritasPrep
- GMAT Instructor
- Posts: 2630
- Joined: Wed Sep 12, 2012 3:32 pm
- Location: East Bay all the way
- Thanked: 625 times
- Followed by:119 members
- GMAT Score:780
I tried to illustrate this (picture attached), but here's the basic logic:
If a line runs through the midpoints of two sides of a triangle, that line is PARALLEL to the third side of the triangle. So XY is parallel to AB, and RS is parallel to XY.
Since AB, XY, and RS are parallel to one another, they make the same angles where they meet sides AC and BC, respectively, so we have three similar triangles: ABC, XYC, and RSC. Since RC = 1/4 AC and SC = 1/4 BC, all the dimensions of RSC are 1/4 the respective dimensions of ABC, including the base and height. So if the area of ABC is bh/2, the area of RSC is ((b/4)(h/4))/2, or bh/32, and all we need to solve the problem is the area of ABC.
S1 tells us ABX has an area of 32. From this we can get the area of ABC - SUFFICIENT.
S2 gives us an altitude of ABC, but not the length of its corresponding base. We aren't able to get the area of ABC - INSUFFICIENT.
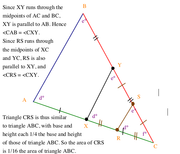
(Problems requiring an understanding of midsegments are uncommon on the GMAT, so I wouldn't sweat this one too much. For more practice on this, check out this link:
https://www.regentsprep.org/Regents/math ... dLineL.htm)
If a line runs through the midpoints of two sides of a triangle, that line is PARALLEL to the third side of the triangle. So XY is parallel to AB, and RS is parallel to XY.
Since AB, XY, and RS are parallel to one another, they make the same angles where they meet sides AC and BC, respectively, so we have three similar triangles: ABC, XYC, and RSC. Since RC = 1/4 AC and SC = 1/4 BC, all the dimensions of RSC are 1/4 the respective dimensions of ABC, including the base and height. So if the area of ABC is bh/2, the area of RSC is ((b/4)(h/4))/2, or bh/32, and all we need to solve the problem is the area of ABC.
S1 tells us ABX has an area of 32. From this we can get the area of ABC - SUFFICIENT.
S2 gives us an altitude of ABC, but not the length of its corresponding base. We aren't able to get the area of ABC - INSUFFICIENT.

(Problems requiring an understanding of midsegments are uncommon on the GMAT, so I wouldn't sweat this one too much. For more practice on this, check out this link:
https://www.regentsprep.org/Regents/math ... dLineL.htm)
- GMATGuruNY
- GMAT Instructor
- Posts: 15539
- Joined: Tue May 25, 2010 12:04 pm
- Location: New York, NY
- Thanked: 13060 times
- Followed by:1906 members
- GMAT Score:790
In triangle ABC, point X is the midpoint of side AC and point Y is the midpoint of side BC. If point R is the midpoint of line segment XC and if point S is the midpoint of line segment YC, what is the area of triangular region RCS ?
(1) The area of triangular region ABX is 32.
(2) The length of one of the altitudes of triangle ABC is 8.

Triangles RCS and ABC:
Side RC = 1/4(AC).
Side SC = 1/4(BC).
The two triangles share angle BCA.
Triangles with a shared angle (BCA) formed by corresponding sides in the same proportion (RC:AC = 1:4, SC:BC = 1:4) are SIMILAR.
Thus, triangle RCS is similar to triangle ABC.
In similar triangles, corresponding bases and heights are in the same proportion as corresponding sides.
Thus, the base of triangle RCS is 1/4 the base of triangle ABC, and the height of triangle RCS is 1/4 the height of triangle ABC.
Area of triangle ABC = (1/2)bh.
Area of triangle RCS = (1/2)*1/4(b)*1/4(h) = (1/16)(1/2)bh.
Thus, the area of triangle RCS is 1/16 the area of triangle ABC.
Question rephrased: What is the area of triangle ABC?
Statement 1: ABX = 32.

In triangle ABX, AX = 1/2(AC).
In other words, the base of triangle ABX is 1/2 the base of triangle ABC.
Triangles ABX and ABC share height BZ.
Since AX = 1/2(AC), and the two triangles have the same height, ABX = 1/2(ABC).
Thus, the area of triangle ABC = 64, and the area of triangle RCS = (1/16)(64) = 4.
SUFFICIENT.
Statement 2: height = 8.
No way to determine the area of triangle ABC or of triangle RCS.
INSUFFICIENT.
The correct answer is A.
Private tutor exclusively for the GMAT and GRE, with over 20 years of experience.
Followed here and elsewhere by over 1900 test-takers.
I have worked with students based in the US, Australia, Taiwan, China, Tajikistan, Kuwait, Saudi Arabia -- a long list of countries.
My students have been admitted to HBS, CBS, Tuck, Yale, Stern, Fuqua -- a long list of top programs.
As a tutor, I don't simply teach you how I would approach problems.
I unlock the best way for YOU to solve problems.
For more information, please email me (Mitch Hunt) at [email protected].
Student Review #1
Student Review #2
Student Review #3
Followed here and elsewhere by over 1900 test-takers.
I have worked with students based in the US, Australia, Taiwan, China, Tajikistan, Kuwait, Saudi Arabia -- a long list of countries.
My students have been admitted to HBS, CBS, Tuck, Yale, Stern, Fuqua -- a long list of top programs.
As a tutor, I don't simply teach you how I would approach problems.
I unlock the best way for YOU to solve problems.
For more information, please email me (Mitch Hunt) at [email protected].
Student Review #1
Student Review #2
Student Review #3
-
[email protected]
- Master | Next Rank: 500 Posts
- Posts: 429
- Joined: Wed Sep 19, 2012 11:38 pm
- Thanked: 6 times
- Followed by:4 members
Hey Mitch, what I dont understand is that how u got the altitude BZ, i.e ABZ is a rigth angle triangle!
Thanks
Shiba
Thanks
Shiba
-
GaneshMalkar
- Senior | Next Rank: 100 Posts
- Posts: 77
- Joined: Tue Jul 31, 2012 6:53 am
- Thanked: 8 times
- Followed by:1 members
BZ is the perpendicular drop from the point B to the extended base AC which is the height or altitude of triangle ABC.[email protected] wrote:Hey Mitch, what I dont understand is that how u got the altitude BZ, i.e ABZ is a rigth angle triangle!
Thanks
Shiba
If you cant explain it simply you dont understand it well enough!!!
- Genius
- Genius
-
Nina1987
- Senior | Next Rank: 100 Posts
- Posts: 79
- Joined: Tue Dec 15, 2015 3:56 am
- Followed by:1 members
- GMAT Score:750
The question is testing properties of similar triangles here. There 3 ways to tell if the triangles are similar:
1. AAA (angle angle angle)
All three pairs of corresponding angles are the same.
(We actually need two angles really:)
2. SSS in same proportion (side side side)
All three pairs of corresponding sides are in the same proportion
3. SAS (side angle side)
Two pairs of sides in the same proportion and the included angle equal.
It is this 3rd property that is quite handy here. Two triangles ABC and RSC are similar since RC/AC=SC/BC=1/4 and they include the same angle THETA (as shown in the figure)
1) Tells us that Area(ABX) =32. Since height of triangle ABC is same that of triangle ABX and the base is twice, area (ABC) = 32*2= 64. Since ABC and RSC are similar and their sides are in the ration of 1:4 their ares will be in the ration of 1:16. Sufficient to solve.
2) Tells us one of the altitudes is 8. Since it does not tell which one, insufficient!
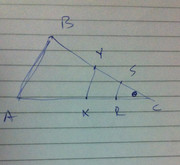
1. AAA (angle angle angle)
All three pairs of corresponding angles are the same.
(We actually need two angles really:)
2. SSS in same proportion (side side side)
All three pairs of corresponding sides are in the same proportion
3. SAS (side angle side)
Two pairs of sides in the same proportion and the included angle equal.
It is this 3rd property that is quite handy here. Two triangles ABC and RSC are similar since RC/AC=SC/BC=1/4 and they include the same angle THETA (as shown in the figure)
1) Tells us that Area(ABX) =32. Since height of triangle ABC is same that of triangle ABX and the base is twice, area (ABC) = 32*2= 64. Since ABC and RSC are similar and their sides are in the ration of 1:4 their ares will be in the ration of 1:16. Sufficient to solve.
2) Tells us one of the altitudes is 8. Since it does not tell which one, insufficient!




















