Each light bulb at Hotel California is either incandescent or fluorescent. At a certain moment, forty percent of the incandescent bulbs are switched on, and ten percent of the fluorescent bulbs are switched off. If eighty percent of all the bulbs are switched on at this moment, what percent of the bulbs that are switched on are incandescent?
22 (2/9)%
16 (2/3)%
11 (1/9)%
10%
5%
MGMAT
This topic has expert replies
-
alltimeacheiver
- Master | Next Rank: 500 Posts
- Posts: 183
- Joined: Wed Feb 09, 2011 3:08 am
- Location: Delhi
- Thanked: 1 times
- Followed by:5 members
- manpsingh87
- Master | Next Rank: 500 Posts
- Posts: 436
- Joined: Tue Feb 08, 2011 3:07 am
- Thanked: 72 times
- Followed by:6 members
hi this problem is similar to the following problem,,, please go through it for detailed solution..!!!alltimeacheiver wrote:Each light bulb at Hotel California is either incandescent or fluorescent. At a certain moment, forty percent of the incandescent bulbs are switched on, and ten percent of the fluorescent bulbs are switched off. If eighty percent of all the bulbs are switched on at this moment, what percent of the bulbs that are switched on are incandescent?
22 (2/9)%
16 (2/3)%
11 (1/9)%
10%
5%
https://www.beatthegmat.com/how-many-bul ... 82382.html
O Excellence... my search for you is on... you can be far.. but not beyond my reach!
- GMATGuruNY
- GMAT Instructor
- Posts: 15539
- Joined: Tue May 25, 2010 12:04 pm
- Location: New York, NY
- Thanked: 13060 times
- Followed by:1906 members
- GMAT Score:790
Like many GMAT problems, the one above can be solved with clever reasoning and perhaps some trial and error.alltimeacheiver wrote:Each light bulb at Hotel California is either incandescent or fluorescent. At a certain moment, forty percent of the incandescent bulbs are switched on, and ten percent of the fluorescent bulbs are switched off. If eighty percent of all the bulbs are switched on at this moment, what percent of the bulbs that are switched on are incandescent?
22 (2/9)%
16 (2/3)%
11 (1/9)%
10%
5%
Let total bulbs = 100.
Number of bulbs on = .8*100 = 80.
Since 80 bulbs are on, and 90% of the fluorescent bulbs are switched on, the number of fluorescent bulbs must be very high.
We know that 90 fluorescent bulbs would be too many, because with 10% of these switched off, the number switched on would be 90-9 = 81, 1 more than the 80 that are supposed to be switched on.
Let fluorescent = 80.
10% of these switched off = 8 off, 72 on.
Incandescent = 100-80 = 20.
40% of these switched on = 8 on, 12 off.
Total on = 72+8 = 80. This works.
Thus, of the 80 bulbs that are switched on, 8 are incandescent.
8/80 = 10%.
The correct answer is D.
Here's the algebraic approach:
Let total bulbs = 100.
Let x = incandescent bulbs.
Let 100-x = fluorescent bulbs.
40% of the incandescent bulbs switched on = .4x
10% of the fluorescent bulbs switched off = 90% switched on = .9(100-x).
Since .8*100 = 80 bulbs are switched on, we get:
.4x + .9(100-x) = 80.
4x + 900 - 9x = 800
-5x = -100
x = 20.
Thus, .4*20 = 8 of the incandescent bulbs are switched on.
Incandescent on/Total on = 8/80 = 10%.
Private tutor exclusively for the GMAT and GRE, with over 20 years of experience.
Followed here and elsewhere by over 1900 test-takers.
I have worked with students based in the US, Australia, Taiwan, China, Tajikistan, Kuwait, Saudi Arabia -- a long list of countries.
My students have been admitted to HBS, CBS, Tuck, Yale, Stern, Fuqua -- a long list of top programs.
As a tutor, I don't simply teach you how I would approach problems.
I unlock the best way for YOU to solve problems.
For more information, please email me (Mitch Hunt) at [email protected].
Student Review #1
Student Review #2
Student Review #3
Followed here and elsewhere by over 1900 test-takers.
I have worked with students based in the US, Australia, Taiwan, China, Tajikistan, Kuwait, Saudi Arabia -- a long list of countries.
My students have been admitted to HBS, CBS, Tuck, Yale, Stern, Fuqua -- a long list of top programs.
As a tutor, I don't simply teach you how I would approach problems.
I unlock the best way for YOU to solve problems.
For more information, please email me (Mitch Hunt) at [email protected].
Student Review #1
Student Review #2
Student Review #3
-
winniethepooh
- Master | Next Rank: 500 Posts
- Posts: 370
- Joined: Sat Jun 11, 2011 8:50 pm
- Location: Arlington, MA.
- Thanked: 27 times
- Followed by:2 members
Hi Mitch, I am just wondering why didn't you take incandescent bulb as x and florescent as y??
Why did you florescent to be 100-x?
Also, why don't we get the correct answer by equating these two equations:
Say, incan =x
and Floro =y
ad total bulbs be 100.
Therefore, .4x+.9y=80___(1)
and .6x+y=20
Why did you florescent to be 100-x?
Also, why don't we get the correct answer by equating these two equations:
Say, incan =x
and Floro =y
ad total bulbs be 100.
Therefore, .4x+.9y=80___(1)
and .6x+y=20
- GMATGuruNY
- GMAT Instructor
- Posts: 15539
- Joined: Tue May 25, 2010 12:04 pm
- Location: New York, NY
- Thanked: 13060 times
- Followed by:1906 members
- GMAT Score:790
We could do the following:winniethepooh wrote:Hi Mitch, I am just wondering why didn't you take incandescent bulb as x and florescent as y??
Why did you florescent to be 100-x?
Also, why don't we get the correct answer by equating these two equations:
Say, incan =x
and Floro =y
ad total bulbs be 100.
Therefore, .4x+.9y=80___(1)
and .6x+y=20
Let i = the number of incandescent bulbs.
Let f = the number of fluorescent bulbs.
If there are 100 bulbs:
i+f = 100.
Since 40% of the incandescents are switched on, 90% of the fluorescents are switched on, and 80 bulbs in total are switched on, we get:
.4i + .9f = 80.
Rephrasing the equations, we get:
i+f = 100 ---> 9i+9f = 900.
.4i + .9f = 80 ---> 4i+9f = 800.
Subtracting the second equation from the first, we get:
5i = 100.
i = 20.
Thus, the number of incandescent bulbs switched on = .4(20) = 8.
Thus, (incandescent on)/(total on) = 8/80 = 10%.
Private tutor exclusively for the GMAT and GRE, with over 20 years of experience.
Followed here and elsewhere by over 1900 test-takers.
I have worked with students based in the US, Australia, Taiwan, China, Tajikistan, Kuwait, Saudi Arabia -- a long list of countries.
My students have been admitted to HBS, CBS, Tuck, Yale, Stern, Fuqua -- a long list of top programs.
As a tutor, I don't simply teach you how I would approach problems.
I unlock the best way for YOU to solve problems.
For more information, please email me (Mitch Hunt) at [email protected].
Student Review #1
Student Review #2
Student Review #3
Followed here and elsewhere by over 1900 test-takers.
I have worked with students based in the US, Australia, Taiwan, China, Tajikistan, Kuwait, Saudi Arabia -- a long list of countries.
My students have been admitted to HBS, CBS, Tuck, Yale, Stern, Fuqua -- a long list of top programs.
As a tutor, I don't simply teach you how I would approach problems.
I unlock the best way for YOU to solve problems.
For more information, please email me (Mitch Hunt) at [email protected].
Student Review #1
Student Review #2
Student Review #3
- [email protected]
- Legendary Member
- Posts: 934
- Joined: Tue Nov 09, 2010 5:16 am
- Location: AAMCHI MUMBAI LOCAL
- Thanked: 63 times
- Followed by:14 members
Yes by simultaneous equations, you get two equations and you get the answer as 10%
equation 1: x + y = 100
equation 2: .40x + .90y = 80
solving both we get what we need...
Hope this helps...
equation 1: x + y = 100
equation 2: .40x + .90y = 80
solving both we get what we need...
Hope this helps...
IT IS TIME TO BEAT THE GMAT
LEARNING, APPLICATION AND TIMING IS THE FACT OF GMAT AND LIFE AS WELL... KEEP PLAYING!!!
Whenever you feel that my post really helped you to learn something new, please press on the 'THANK' button.
LEARNING, APPLICATION AND TIMING IS THE FACT OF GMAT AND LIFE AS WELL... KEEP PLAYING!!!
Whenever you feel that my post really helped you to learn something new, please press on the 'THANK' button.
GMAT/MBA Expert
- Whitney Garner
- GMAT Instructor
- Posts: 273
- Joined: Tue Sep 21, 2010 5:37 am
- Location: Raleigh, NC
- Thanked: 154 times
- Followed by:74 members
- GMAT Score:770
I'll argue that the easiest way to deal with these types of problems is to use a Grid (we call it a Double-Set Matrix in the book). The idea is to recognize the problem type as one that presents you with 2 MECE pairs...alltimeacheiver wrote:Each light bulb at Hotel California is either incandescent or fluorescent. At a certain moment, forty percent of the incandescent bulbs are switched on, and ten percent of the fluorescent bulbs are switched off. If eighty percent of all the bulbs are switched on at this moment, what percent of the bulbs that are switched on are incandescent?
22 (2/9)%
16 (2/3)%
11 (1/9)%
10%
5%
What is a MECE Pair?
- Let's start with the meaning of MECE (Mututally Exclusive, Collectively Exhaustive).
So, if I group data and I want to make sure those categories are MECE, then they must be:
Mutually Exclusive - if you belong to one group, you cannot belong to the other
Collectively Exhaustive - everyone belongs to one of the groups.
We can think of a MECE pair like a light switch (pardon the similarity to the current question). A MECE pair would be like a light switch turning a quality ON and OFF. Some example MECE pairs would be the following:
Male/Female, Night/Day, Pass/Fail, Nocturnal/Diurnal, Cat/Not-Cat (notice that it isn't Cat/Dog because there are plenty of other categories besides Cat and Dog that things can fall into).
So let's get back to our example. We are talking about Light Bulbs. What are the characteristics that can be turned On or Off??
(1) The lights can be On or OFF (okay, then that is one MECE Pair).
(2) The lights can be either Incandescent or Fluorescent (there is our second pair).
Then we build a 3x3 matrix where we put 1 pair across the top and one down the side:
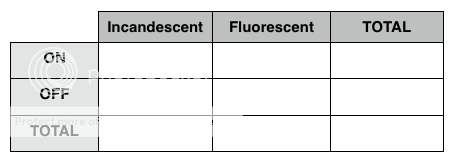
Notice that in every row and column, we can fill in information by looking at the cross-listings. For example, the number of Incandescent lights that are ON would be the top left box, and the TOTAL number of lights that are ON would be the top right!
We can also see that columns add down to give totals, and rows add across - pretty handy!
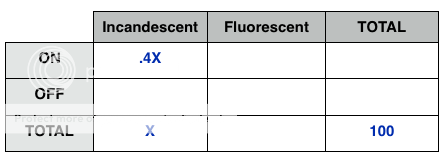
Now, because the original problem talks only of percents and gives no real numbers, let's use a smart number to represent the TOTAL number of light bulbs = 100.
Now we fill in the rest:
40% of Incandescent are ON (do we know the total number of incandescent? No, we will need a variable, and then we can take 40% of it (40% of X = .4X)!
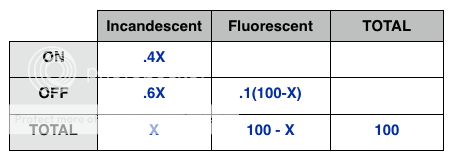
Then we can use addition and subtraction to fill in a few additional boxes:

10% of the fluorescent bulbs are OFF (well, we know now that this is 100-x, so we can use .1*(100-x) for that box).
Finally, we know that 80% of ALL bulbs are ON. This means 80 of our 100 are on.
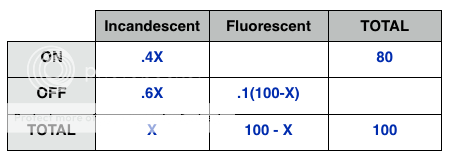
Use addition and subtraction to fill in the other boxes (we really only need enough to have a completed row).
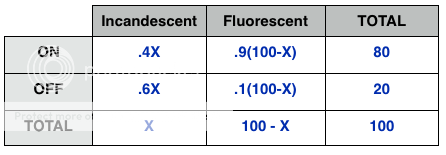
Now we can use EITHER row to solve for X:
.6X + .1(100-X) = 20
.6X + 10 - .1X = 20
.5X = 10
5X = 100
X = 20
But we don't just want the number of incandescent bulbs. We actually want to know what percent of the ON bulbs are Incandescent. Well, that would be .4X/80 = 4X/800 = X/200 = 20/200 = 10/100 = 10%!
This explanation might seem a bit long, but building and filling in your own table is actually quite quick!!
Hope this helps!
Whit
Whitney Garner
GMAT Instructor & Instructor Developer
Manhattan Prep
Contributor to Beat The GMAT!
Math is a lot like love - a simple idea that can easily get complicated
GMAT Instructor & Instructor Developer
Manhattan Prep
Contributor to Beat The GMAT!
Math is a lot like love - a simple idea that can easily get complicated



















