Breaking Down GMATPrep Average + Arithmetic Problems
In the past, weve discussed weighted average Data Sufficiency problems (twice: first here and then here) and weve also discussed how to turn algebra problems into arithmetic problems. This week, were going to put these concepts together. Weve got a GMATPrep weighted average Problem Solving question that qualifies for the arithmetic method.
Weighted average problems on the GMAT are more often DS questions, but they can appear in PS format as well (as we see below). Decide whether you want to read the previous two articles first, in order to get a better idea of how these problems work. Or try the below first and only go back to the two previous articles if you think you need to (or want to) after youre done.
Heres the GMATPrep problem. Set your timer for 2 minutes. and GO!
Three grades of milk are 1 percent, 2 percent, and 3 percent fat by volume. If x gallons of the 1 percent grade, y gallons of the 2 percent grade, and z gallons of the 3 percent grade are mixed to give x + y + z gallons of a 1.5 percent grade, what is x in terms of y and z?(A) y + 3z
(B) [pmath]{y+z}/4[/pmath]
(C) 2y + 3z
(D) 3y + z
(E) 3y + 4.5z
There are three kinds of milk: 1% milk, 2% milk, and 3% milk. These are our three sub-groups. When the three are combined (in some unknown amounts), we get a 4th kind:1.5% milk. The number of gallons of 1% milk (x), the number of gallons of 2% milk (y) and the number of gallons of 3% milk (z) will add up to the number of gallons of 1.5% milk (x + y + z). Were supposed to figure out what x is, but not the actual value of x rather, were supposed to figure out x in terms of, or using, y and z.
This problem never mentions the word "average". Thats annoying how are we supposed to tell that this is a weighted average problem? Basically, the problem should talk about 2 or 3 sub-groups that are combined in some way to make an overall group, or mixture of the original sub-groups. The problem will often discuss these groups in terms of percentages (as this problem does) or ratios. That starts to tell us that some kind of averaging is happening.
Next, we glance at the answers and notice that there are variable expressions there. Excellent! That means that we can turn this problem into an arithmetic problem if we want we can choose real numbers. As a general rule, we want to do this on harder questions, and weighted average questions tend to be harder questions. Note that there is a super shortcut on this problem, but you really have to understand how weighted averages work in order to use it. So, first, were going to talk about the longer arithmetic method.
Now, we have to come up with some numbers for our variables. Are we going to pick numbers for all three of the variables? Or only for some of them? How do we know?
We need to pick numbers for two of the variables and then do some math; that math will determine the value for the third variable. Which variables do you think would be the easiest ones to use? What kinds of numbers do we need to pick?
The overall average is 1.5% milk, so are we going to need more of the 1% milk, the 2% milk, or the 3% milk? We need more of the 1% than the other two, because its the only one that pulls the average down. Were figuring this out just so that we have a reality check on the problem that will help us pick numbers and also help us know if we did something wrong (for instance, if the calculation tells us that the amount of 1% milk is not the greatest).
Next, we should make use of the fact that the problem asks us to figure out x in terms of, or using, y and z. We can pick nice numbers for two of the variables, but were not sure what kind of number well get for the third it might be a fraction. Were eventually going to have to plug the values for y and z into the answers. So, lets pick nice numbers for y and z; it wont matter as much if x is not as nice a number.
Lets say we have 2 gallons of z (the 3% milk) and 4 gallons of y (the 2% milk), and x gallons of the 1% milk. Total, we have 6 + x gallons of milk. The weighted average is:
[pmath]{x(1)+4(2)+2(3)}/{6+x}=1.5[/pmath]
The numerator consists of each type of milk (1, 2, and 3) multiplied by the number of gallons of that type of milk. Note that I didnt write the three percentages as actual percentages. We just need to keep all of the percentages in the same form 1, 2, 3, and the average percentage, 1.5.
The denominator consists of the total number of gallons: x + 4 + 2, or x + 6.
Now, lets solve for x! First, lets cross-multiply:
[pmath]x+8+6=9+1.5x[/pmath]
[pmath]14-9=1.5x-x[/pmath]
[pmath]5=0.5x[/pmath]
[pmath]x=10[/pmath]
Hey, x turned out to be an easy number thats great! (Note: these really were the first numbers that I tried and I didnt even try to find something that would make x nice; I just got lucky. If I hadnt gotten a nice number for x, I wouldnt have cared. Id just keep going with the below.)
Now, Im going to test y=4 and z=2 in the answer choices, looking for the value 10.
(A) y + 3z = 4 + 3(2) = 10 Bingo!
(B) (y+z)/4=(4+2)/4<>10 (stop calculating when you can tell it wont be 10)
(C) 2y + 3z = 2(4) + 3(2) = too big
(D) 3y + z = 3(4) + stop! too big
(E) 3y + 4.5z = 3(4) + stop! too big
The correct answer is A.
Okay, do you want the super shortcut? If you havent yet read the second of the two previous weighted average articles (linked at the beginning of this article), do so now. Im not going to explain fully how this all works here its already in the other article. First, draw a number line that represents what we know to start:
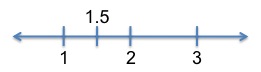
We have three different kinds of milk to start, represented by the three numbers underneath the number line. The desired (final) weighted average is represented by the number on top, 1.5.
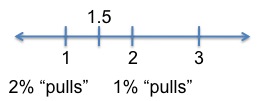
The 1% milk has to pull the average toward it and away from the 2% and 3% milks. Compare the 1% and 2% milk first. The 1% milk pulls the average 0.5 units away from 2 and towards 1, so the 1% milks weighting relative to the 2% milk is 0.5. Likewise, the 2% milk, pulls the average 0.5 units away from 1 and towards 2, so the 2% milks weighting relative to the 1% milk is 0.5. In other words, we need equal amounts of these two milks, x and y. If we have 2x, then we have 2y, and so on.
Now, lets compare the 1% and 3% milk. The 1% milk pulls the average 1.5 units away from 3 and towards 1, so the 1% milks weighting relative to the 3% milk is 1.5. The 3% milk pulls the average 0.5 units away from 1 and towards 3, so the 3% milks weighting relative to the 1% milk is 0.5. In other words, we have 3 times as much x as we do z, because 1.5 is three times 0.5.
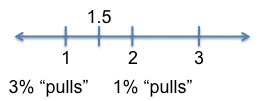
If we want to represent y in terms of x, its easy: the two are equal, so we can just use y in place of x. If we want to represent z in terms of x, its just a little trickier. We want x to be three times greater than z, so we would write x = 3z. Do these terms look at all familiar? Go back and look at answer A: its y + 3z. Done!
Key Takeaways for Problem Solving Average + Arithmetic Problems:
(1) Determine that you have a weighted average problem: this occurs when an average is described (even if the word average is not in the problem!), but that average is not a standard 1:1 or equally weighted average.
(2) Determine that you can turn this problem into arithmetic. This occurs when the answer choices contain variable expressions (no equals sign or inequality). Also, know how to decide whether you want to do so. Typically, the harder the algebra for you, the easier it will be to do arithmetic instead. Most weighted average problems are on the more difficult side.
(3) If you feel very comfortable with weighted averages, you can also use the super shortcut number line method. Note that its very easy to make mistakes with this shortcut; use the arithmetic method if you dont feel very comfortable with the concepts underlying weighted averages.
* GMATPrep questions courtesy of the Graduate Management Admissions Council. Usage of this question does not imply endorsement by GMAC.