Breaking Down a GMATPrep Number Line Theory Problem
This week, were all about number lines: how to think about them and how to avoid traps. I think this one is deceptively tricky. Dont say you havent been warned!
Lets start with the GMATPrep problem. Set your timer for 2 minutes. and GO!
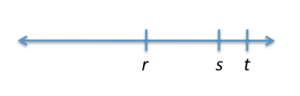
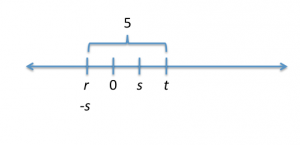
* On the number line shown, is zero halfway between r and s?(1) s is to the right of zero.
(2) The distance between t and r is the same as the distance between t and s.
The first thing youll probably notice: I didnt include the answer choices. The five Data Sufficiency answer choices are always the same, so we should have those memorized. If you dont have them memorized yet, add this to your to do list.
Just in case, here are the five choices (in casual language, not official language):
(A) statement 1 works but statement 2 does not work
(B) statement 2 works but statement 1 does not work
(C) the statements do NOT work alone, but they DO work together
(D) each statement works by itself
(E) nothing works, not even using them together
Okay, now that weve got that out of the way, lets tackle this problem! As I said above, this ones deceptive; we really have to be careful here. Drawing (and labeling what we draw) will be important. Theyre using a number line to ask us about some fairly basic properties of numbers, positive and negative, but the way this one is set up well, its easy to fall into traps.
I have three variables, r, s, and t, shown on the number line, and Im asked a yes/no question about the relationship between r and s. My task is to determine whether I can answer this question always yes, always no, or sometimes yes, sometimes no given various pieces of information in the statements. An always yes or always no answer is sufficient to answer the question. A sometimes yes, sometimes no answer is NOT sufficient to answer the question.
Also, its data sufficiency. Remind yourself that the diagram does NOT need to be drawn to scale. You can trust that r, s, and t do show up in that order relative to each other, but thats all you know. Draw the diagram on your scrap paper as you see it, but remember that you may have to be flexible.
First, I want to decide whether I can figure anything out just from the question stem (before I start addressing the statements). In this case, the question stem asks about the relationship between r and s. Lets say that its true that zero is halfway between the two. What would that mean? Ah, okay, that would mean that [pmath]delim{|}{r}{|}=delim{|}{s}{|}[/pmath]. The magnitude (or the number) of the two would be the same, but r would be negative and s would be positive.
So I could rephrase the question as: does [pmath]delim{|}{r}{|}=delim{|}{s}{|}[/pmath] or I could phrase it as are the magnitudes of r and s equal?" (Choose whatever you prefer.)
Next, I glance at the statements to decide which one I want to address first. Normally, I start with the first one, but if I think the second one is noticeably easier than the first, then Ill start with the second. Do you think one statement is easier on this problem?
Statement 2 definitely doesnt look easier to me, so Im going to start with statement 1. (Note: determining the relative difficulty of the two statements is a somewhat subjective call; different people will disagree and thats okay. Start with the one you think is easier.)
(1) s is to the right of zero.
I have two choices in general on theory problems like this one: I can try some numbers or I can think this through theoretically (if I think I know the theory well enough). It turns out, on this particular statement, that we dont even need to decide between those two.
As soon as I think about trying numbers or about placing the information on the number line, I realize that theyve told me nothing at all about r. This statement cant be sufficient then; I need to know something about both r and s in order to answer the question. Eliminate answers A and D.
Now we have to tackle the more annoying (to me!) statement:
(2) The distance between t and r is the same as the distance between t and s.
If you drew statement 1 on your number line, start working with a fresh number line that does not include the info from statement 1. Remember, that info does not exist right now.
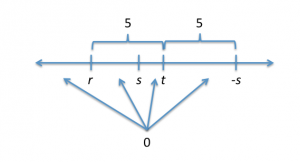
Again, we can try numbers or think things through theoretically (or use a bit of both), and on this one, we do actually have to go through the steps. Lets try numbers first. Hmm. Im going to say the distance theyre talking about is 5. Draw a number line showing the distance from t to r as 5. Now, where are we going to place s?
If 3 were placed on the number line and you needed to place -3, where would you put it? What about if -4 were on the number line and you needed to place (-4)? Right, on the opposite side of zero. Okay. But I dont know where zero is. Oh, but I do know that the distance from t to s also needs to be 5. So one place to put s is right where Ive already placed r. Zero is always halfway between s and s, so if s is where r is, then zero is also halfway between r and s! In this example, at least, the information is sufficient to answer the question yes.
Is the information sufficient to answer the question always yes? We still need to figure that out. And heres where trying numbers on this one is going to get a bit tricky. How do I know which numbers to pick next? If I want to make my job easier, I actually do need to try to figure some things out about the theory. So were going to use a hybrid approach on this one: a bit of both trying numbers and thinking about theory.
There are exactly two places where I can place s: where r is, or on the other side of t, to the right. I just tried the option where we would place s on the same spot as r, but what about that other option? Draw it.
[Note: we just passed the first big trap: assuming that s must be placed to the left of s. Thats not necessarily true. The plain s could be the negative number, and then the s would turn into the positive number!]
So in this new scenario, with s to the right of t, where would zero go?
There are four possibilities: to the left of r, between r and s, between r and t, or to the right of t.
What next? Wherever I place s, zero has to be halfway between s and s. The placement of s, then, determines the placement of zero. In this scenario, zero has to be either between s and t or between t and s. The distance between the two is somewhat longer than the distance between t and s, so its larger than 5. Lets call it 6. Where would zero be, then?
Halfway between:
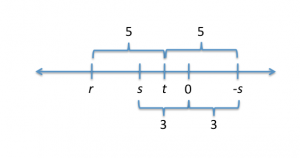
Now, does this fit all of the constraints given by the original diagram (in terms of the order of r, s, and t on the number line) and statement 2?
It does! Excellent. For this scenario, the answer to our question is no. With a yes and a no, we now know that statement 2 is insufficient. Eliminate answer B.
Now, we need to test the two statements together. Im going to use my thinking about statement 2 as my starting point, but now I have to place zero to the left of s. That means our last little scenario cant be used any longer, because zero is not to the left of s in that scenario.
Heres what were left with:
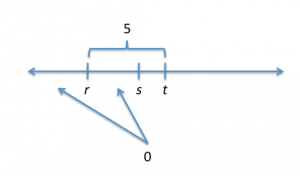
What does that tell us about the placement of s? Well, -s has to be on the other side of zero than s, so s must be somewhere to the left. What did we say earlier about the possible placements for s?
Originally, there were only two: either 5 units to the right of t or 5 units to the left of t (and exactly where r is). With both statements together, only one of those options still exists: -s must be exactly where r is. If thats the case, then zero must be halfway between r and s because zero must be halfway between s and s.
The correct answer is C.
The biggest trap answer on this problem is B. If you forget to try both configurations for the placement of s, OR if you think that s must represent the negative number and therefore be placed to the left of s, OR if you mistakenly forget to forget statement 1 when evaluating statement 2 any one of those mistakes will cause you to pick B.
Key Takeaways for Solving Number Line Problems:
(1) Draw some lines! Think about all of the possible configurations, given one piece of info, and draw them all. Try to think of the possible configurations every time youre given a new piece of info, before you start testing scenarios or evaluating.
(2) Remember that a variable can represent any number, negative, positive or zero. A negative sign in front of the variable does not mean that the "plain" variable represents a positive number. The "plain" variable could be a negative number and sticking that negative sign in front will then turn it positive!
* GMATPrep questions courtesy of the Graduate Management Admissions Council. Usage of this question does not imply endorsement by GMAC.