Translating Words into Math
Ive spoken with several students recently who are struggling with translating wordy quant problems into the actual math necessary to set up and solve the problem. Some people make too many mistakes when doing this, and others find that, though generally accurate, they take more time than they can afford. In the next two articles (this is part 1!), were going to talk about how to translate efficiently and effectively.
Were going to do this by example: Ill provide short excerpts from OG or GMATPrep problems, and then well discuss how to know what to do, how to do the actual translation, and how to do so efficiently. Note that Im not going to provide the full text of problems and, therefore, were not going to solve fully. Thats not our goal today.
The Basics
Before we dive into more advanced issues, there are some basics we all need to know. Were not going to spend a lot of time on the basics because all GMAT books out there already explain this; Ill give a quick introduction and, if you need more, seek out one of the standard books on this topic (in ManhattanGMATs books, youll find this info in the Algebraic Translations chapter of the Word Translations Strategy Guide).
First, when the problem introduces certain people, objects or other things, we will likely need to assign variables. Cindy can become C and Bob can become B. Next, the words will give us some kind of relationship between variables.
For instance, a sentence might tell us that Cindy is five years older than Bob. Weve already decided to use C for Cindy and B for B. Next, the is represents an equals sign. Five, of course, represents the number 5. Finally older than indicates addition; we need a plus sign. Our translated equation becomes C = 5+B. (Another very common word is of, which typically means to multiply. For example, of 6 would be written: 6.)
Notice a couple of things about this equation. We have two unknowns in the sentence, so we should expect to have two variables in the equation. Also, how can we quickly check the equation to see that it makes sense? There are two common ways. We can plug in some simple numbers to test the equation this might take a little bit longer, but its the more certain method. Or we can think about the concepts that have been presented. Whos older and whos younger? To which person do we need to add years in order to make their ages equal? We want to add to the younger in order to equal the older. Bobs the younger one, so we want to add to his age. Does the equation do that?
Heres an excerpt from an official question, Problem Solving (PS) problem #120 in the Official Guide 12th Edition (OG12):
David has d books, which is 3 times as many as Jeff and as many as Paula.
Theyve already defined one variable for us: d for the number of books David has. Lets use j for Jeffs books and p for Paulas books.
Next, take each piece of info separately:
David has d books, and d is (=) 3 times as many as (multiply) j, or d = 3j.
David has d books, and d is (=) [pmath]1/2[/pmath] as many as (multiply) p, or d = [pmath]1/2[/pmath].
Task 1: translate everything and make it real
In OG12, PS problem #91 first tells us that a store sells all of its maps at one specific price and all of its books at another specific price. It also tells us:
On Monday, the store sold 12 maps and 10 books for a total of $38.00, and on Tuesday the store sold 20 maps and 15 books for a total of $60.00.
What should we do? First, set variables. Let m = the price for one map and let b = the price for one book. Then, pretend you own the store and a customer walks up with 12 maps and 10 books. What do you do? Make it real actually visualize (or draw out) what needs to happen.
First, Id figure out how much I need to charge for the maps: $m each for 12 = 12m. Similarly, the books would cost 10b. You want to buy all of them? Excellent! You owe me 12m + 10b = 38. If we do the same thing with the second half of the sentence quoted above, we get 20m + 15b = 60.
So, were done with that now, we need to solve for m and b, right? Not so fast! Read the actual question first:
How much less does a map sell for than a book?
Hmm. Theyre not just asking for the price of a map or the price of a book. Theyre asking for the difference (less than) between the two. Which one costs more and which one costs less?
The sentence is telling us that the map is cheaper. Okay, so if I want the difference in cost between a book and a map, and the map is the cheaper item, how do I do that subtraction? Right, b m. I actually want to solve for that overall combination (b m); if I can find a way to do that without solving for b and m individually first, I can save time! (That topic, however, well save for another time.)
Task 2: Where appropriate, use a chart or table to organize
Lets try another; this is excerpted from PS #154 from OG12:
An empty pool being filled with water at a constant rate takes 8 hours to fill to 3/5 of its capacity.
Again, visualize youre standing there (for 8 hours!) with the hose, watching the pool fill. How does it work? RTW: Rate Time = Work. Make a chart:
Okay, so we have one formula: R 8 = 3/5. The next sentence says:
How much more time will it take to finish filling the pool?
To finish filling hmm, how much more do we have to fill? An entire job = 1. Weve filled 3/5, so we have 2/5 to go, right? Add another row to your chart:
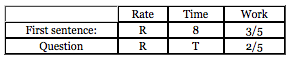
Hey, weve got another formula: RT = 2/5. We can use the first one to solve for R, then plug into the second to solve for T.
One more! Lets try this excerpt from PS #153 from OG12:
Jack is now 14 years older than Bill. If in 10 years Jack will be twice as old as Bill, how old will Jack be in 5 years?
First, set a chart up. We need a row for each person in the problem, and we also need to represent all of the timeframes that are discussed. Careful there are three timeframes, not two!
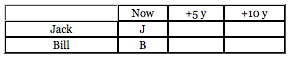
Assign variables decide whether to use one variable or two and decide when to set each base variable (most of the time, well set the base variable to the Now timeframe). In the above chart, Ive set two variables in the Now timeframe.
Next, if you want to use one variable, try to use the simplest piece of information given in the problem to simplify to one variable. In this case, the first sentence is the simplest info because it is set in the Now timeframe for both Jack and Bill.
Jack is now 14 years older than Bill.
J = 14 + B
Remember, is means equals and older than means add. Do you remember how to check your equation quickly to make sure it makes sense?
Whos older, Jack or Bill? According to the sentence, Jack. The equation adds the 14 to the younger person, Bill. That makes sense.
Okay, so we can either remove the J from our table and insert 14 + B instead, or we can flip the equation around (to J 14 = B), then remove B from the table and insert J 14 instead. Does it matter? Mathematically, no, but practically speaking, yes make your life easy by keeping the variable for which you want to solve! We want to solve for Jack, so our new table looks like this:
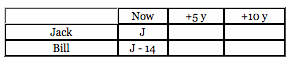
Now fill in the remaining timeframes (you have the info to do this already just add 5 for the middle column and 10 for the final column!):
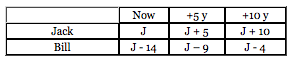
What now? Oh, right now we have that harder second statement to translate:
If in 10 years Jack will be twice as old as Bill
Okay, what timeframe do we need to use? in 10 years okay, go to that column. In 10 years, Jack is J + 10 and Bill is J 4. Make sure to use these as you translate.
Next, will be is a variation of is and means equals. Twice means 2, and as old as means multiply. Heres the translated equation:
J + 10 = 2(J 4)
Hey, we have an equation with one variable! Now we can solve.
Thats all for today; make sure to check back in next week for more (click here to read Part 2), including how the test-writers will disguise the topic area being tested (and how we can recognize what to do anyway!).
Key Takeaways for Translating:
(1) Know the basics. Certain words consistently mean the same thing (for example, forms of the verb to be generally mean equals). There are lots of great resources out there already that will give you the basics.
(2) Those annoying wordy problems have a lot going on. Make sure you are translating every last thing, and also try to make it real! Insert yourself into the situation; imagine that you are the one doing whatevers happening and ask yourself what youd have to do at each step along the way.
(3) When there are multiple variables, multiple timeframes, or other kinds of moving parts, use a chart or table to organize your info. Label everything clearly and only then start filling in.
* GMATPrep text courtesy of the Graduate Management Admissions Council. Usage of this text does not imply endorsement by GMAC.
* The text excerpted above from The Official Guide for GMAT Review 12th Edition is copyright GMAC (the Graduate Management Admissions Council). The short excerpts are quoted under fair-use statutes for scholarly or journalistic work; use of these excerpts does not imply endorsement of this article by GMAC.