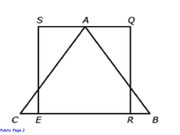
Which area is greater?
This topic has expert replies
GMAT/MBA Expert
- [email protected]
- Elite Legendary Member
- Posts: 10392
- Joined: Sun Jun 23, 2013 6:38 pm
- Location: Palo Alto, CA
- Thanked: 2867 times
- Followed by:511 members
- GMAT Score:800
Hi april24,
You would likely find it easiest to TEST VALUES on this question. Here are some hints to get you started:
There are some rules to remember about the shapes involved:
1) You're dealing with a square, so the base and the height are the SAME
2) Area of a triangle = (1/2)(base)(height).
3) In this prompt, the height of the triangle EQUALS the height of the square
4) In this prompt, the triangle is ISOSCELES.
Try starting with a small value for the side of the square (e.g. 1 or 2) and work through the possibilities from there. Remember that you're looking to prove that the answer to the question is either consistent or inconsistent.
GMAT assassins aren't born, they're made,
Rich
You would likely find it easiest to TEST VALUES on this question. Here are some hints to get you started:
There are some rules to remember about the shapes involved:
1) You're dealing with a square, so the base and the height are the SAME
2) Area of a triangle = (1/2)(base)(height).
3) In this prompt, the height of the triangle EQUALS the height of the square
4) In this prompt, the triangle is ISOSCELES.
Try starting with a small value for the side of the square (e.g. 1 or 2) and work through the possibilities from there. Remember that you're looking to prove that the answer to the question is either consistent or inconsistent.
GMAT assassins aren't born, they're made,
Rich
- GMATGuruNY
- GMAT Instructor
- Posts: 15539
- Joined: Tue May 25, 2010 12:04 pm
- Location: New York, NY
- Thanked: 13060 times
- Followed by:1906 members
- GMAT Score:790
Private tutor exclusively for the GMAT and GRE, with over 20 years of experience.
Followed here and elsewhere by over 1900 test-takers.
I have worked with students based in the US, Australia, Taiwan, China, Tajikistan, Kuwait, Saudi Arabia -- a long list of countries.
My students have been admitted to HBS, CBS, Tuck, Yale, Stern, Fuqua -- a long list of top programs.
As a tutor, I don't simply teach you how I would approach problems.
I unlock the best way for YOU to solve problems.
For more information, please email me (Mitch Hunt) at [email protected].
Student Review #1
Student Review #2
Student Review #3
Followed here and elsewhere by over 1900 test-takers.
I have worked with students based in the US, Australia, Taiwan, China, Tajikistan, Kuwait, Saudi Arabia -- a long list of countries.
My students have been admitted to HBS, CBS, Tuck, Yale, Stern, Fuqua -- a long list of top programs.
As a tutor, I don't simply teach you how I would approach problems.
I unlock the best way for YOU to solve problems.
For more information, please email me (Mitch Hunt) at [email protected].
Student Review #1
Student Review #2
Student Review #3
- Max@Math Revolution
- Elite Legendary Member
- Posts: 3991
- Joined: Fri Jul 24, 2015 2:28 am
- Location: Las Vegas, USA
- Thanked: 19 times
- Followed by:37 members
There are 2 variables in the isosceles triangle and 1 in a square, so we need 3 variables in order to solve the problem.
There are only 2 equations given from the conditions, so there is high chance (E) will be our answer.
Looking at the conditions together, AC and AB passes through the midpoint of SE and QR, so the area of ABC is always greater that that of square SQRE, so this answers the question 'yes' and is sufficient.
The answer is (C).
For cases where we need 3 more equation, such as original conditions with "3 variables", or "4 variables and 1 equation", or "5 variables and 2 equations", we have 1 equation each in both 1) and 2). Therefore, there is 80% chance that E is the answer (especially about 90% of 2 by 2 questions where there are more than 3 variables), while C has 15% chance. These two are the majority. In case of common mistake type 3,4, the answer may be from A, B or D but there is only 5% chance. Since E is most likely to be the answer using 1) and 2) separately according to DS definition (It saves us time). Obviously there may be cases where the answer is A, B, C or D.
There are only 2 equations given from the conditions, so there is high chance (E) will be our answer.
Looking at the conditions together, AC and AB passes through the midpoint of SE and QR, so the area of ABC is always greater that that of square SQRE, so this answers the question 'yes' and is sufficient.
The answer is (C).
For cases where we need 3 more equation, such as original conditions with "3 variables", or "4 variables and 1 equation", or "5 variables and 2 equations", we have 1 equation each in both 1) and 2). Therefore, there is 80% chance that E is the answer (especially about 90% of 2 by 2 questions where there are more than 3 variables), while C has 15% chance. These two are the majority. In case of common mistake type 3,4, the answer may be from A, B or D but there is only 5% chance. Since E is most likely to be the answer using 1) and 2) separately according to DS definition (It saves us time). Obviously there may be cases where the answer is A, B, C or D.

Math Revolution
The World's Most "Complete" GMAT Math Course!
Score an excellent Q49-51 just like 70% of our students.
[Free] Full on-demand course (7 days) - 100 hours of video lessons, 490 lesson topics, and 2,000 questions.
[Course] Starting $79 for on-demand and $60 for tutoring per hour and $390 only for Live Online.
Email to : [email protected]
- GMATGuruNY
- GMAT Instructor
- Posts: 15539
- Joined: Tue May 25, 2010 12:04 pm
- Location: New York, NY
- Thanked: 13060 times
- Followed by:1906 members
- GMAT Score:790
Similar problem:
Statement 1: The length of RE is 4 times the length of BR.
RE = 4BR implies FIGURE A below:
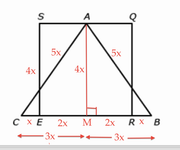
In right triangle ABM, since MB = 3x and AM = 4x, triangle ABM is a 3-4-5 triangle.
Thus, AB = 5x, implying that AC = 5x.
Result:
Perimeter of square SQRE = 4x+4x+4x+4x = 16x.
Perimeter of triangle ABC = 5x+x+2x+2x+x+5x = 16x.
Thus, the difference between the perimeters = 16x-16x = 0.
SUFFICIENT.
Statement 2: The area of triangle ABC is 75% of the area of square SQRE.
In FIGURE A above, the area of triangle ABC is 75% of the area of square SQRE:
(area of triangle ABC)/(area of square SQRE) = (1/2*6x*4x)/(4x*4x) = 12x²/16² = 3/4 = 75%.
Thus, FIGURE A satisfies statement 2.
To determine whether the FIGURE A is the ONLY case that will satisfy statement 2, consider FIGURE B:
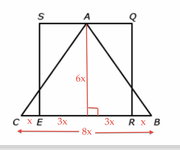
In FIGURE B, RE = 6BR.
Here, (area of triangle ABC)/(area of square SQRE) = (1/2*8x*6x)/(6x*6x) = 24x²/36x² = 2/3 = 66 2/3%.
Doesn't work.
The implication is that, for the area of triangle ABC to be 75% of the area of square SQRE, it must be true that RE=4BR, as in statement 1.
Thus, since statement 1 is sufficient, statement 2 must also be SUFFICIENT.
The correct answer is D.
Alternate way to evaluate Statement 2:
Plug in a value for the side of the square and SOLVE for the dimensions of the triangle.
Square:
Let s = 8.
Area = s² = 8² = 64.
Perimeter = 4s = 4*8 = 32.
Triangle:
Since the area of the triangle is equal to 75% of the area of the square, we get:
Area = (3/4)64 = 48.
As in FIGURE A above, let AM = the height of triangle ABC.
Since AM = 8, we get:
(1/2) * b * 8 = 48.
b = 12.
Thus, MB = (1/2)b = (1/2)12 = 6.
Since MB=6 and AM=8, triangle ABM is a 6-8-10 triangle, implying that AB=10.
Thus:
Perimeter of the triangle = 10+12+10 = 32.
Result:
Perimeter of the square - perimeter of the triangle = 32-32 = 0.
Since AB=AC and AS=AQ, both triangle ABC and square SQRE are SYMMETRICAL about height AM in the figures below.
Statement 1: The length of RE is 4 times the length of BR.
RE = 4BR implies FIGURE A below:

In right triangle ABM, since MB = 3x and AM = 4x, triangle ABM is a 3-4-5 triangle.
Thus, AB = 5x, implying that AC = 5x.
Result:
Perimeter of square SQRE = 4x+4x+4x+4x = 16x.
Perimeter of triangle ABC = 5x+x+2x+2x+x+5x = 16x.
Thus, the difference between the perimeters = 16x-16x = 0.
SUFFICIENT.
Statement 2: The area of triangle ABC is 75% of the area of square SQRE.
In FIGURE A above, the area of triangle ABC is 75% of the area of square SQRE:
(area of triangle ABC)/(area of square SQRE) = (1/2*6x*4x)/(4x*4x) = 12x²/16² = 3/4 = 75%.
Thus, FIGURE A satisfies statement 2.
To determine whether the FIGURE A is the ONLY case that will satisfy statement 2, consider FIGURE B:

In FIGURE B, RE = 6BR.
Here, (area of triangle ABC)/(area of square SQRE) = (1/2*8x*6x)/(6x*6x) = 24x²/36x² = 2/3 = 66 2/3%.
Doesn't work.
The implication is that, for the area of triangle ABC to be 75% of the area of square SQRE, it must be true that RE=4BR, as in statement 1.
Thus, since statement 1 is sufficient, statement 2 must also be SUFFICIENT.
The correct answer is D.
Alternate way to evaluate Statement 2:
Plug in a value for the side of the square and SOLVE for the dimensions of the triangle.
Square:
Let s = 8.
Area = s² = 8² = 64.
Perimeter = 4s = 4*8 = 32.
Triangle:
Since the area of the triangle is equal to 75% of the area of the square, we get:
Area = (3/4)64 = 48.
As in FIGURE A above, let AM = the height of triangle ABC.
Since AM = 8, we get:
(1/2) * b * 8 = 48.
b = 12.
Thus, MB = (1/2)b = (1/2)12 = 6.
Since MB=6 and AM=8, triangle ABM is a 6-8-10 triangle, implying that AB=10.
Thus:
Perimeter of the triangle = 10+12+10 = 32.
Result:
Perimeter of the square - perimeter of the triangle = 32-32 = 0.
Last edited by GMATGuruNY on Sun Nov 15, 2015 5:44 am, edited 1 time in total.
Private tutor exclusively for the GMAT and GRE, with over 20 years of experience.
Followed here and elsewhere by over 1900 test-takers.
I have worked with students based in the US, Australia, Taiwan, China, Tajikistan, Kuwait, Saudi Arabia -- a long list of countries.
My students have been admitted to HBS, CBS, Tuck, Yale, Stern, Fuqua -- a long list of top programs.
As a tutor, I don't simply teach you how I would approach problems.
I unlock the best way for YOU to solve problems.
For more information, please email me (Mitch Hunt) at [email protected].
Student Review #1
Student Review #2
Student Review #3
Followed here and elsewhere by over 1900 test-takers.
I have worked with students based in the US, Australia, Taiwan, China, Tajikistan, Kuwait, Saudi Arabia -- a long list of countries.
My students have been admitted to HBS, CBS, Tuck, Yale, Stern, Fuqua -- a long list of top programs.
As a tutor, I don't simply teach you how I would approach problems.
I unlock the best way for YOU to solve problems.
For more information, please email me (Mitch Hunt) at [email protected].
Student Review #1
Student Review #2
Student Review #3
-
binit
- Master | Next Rank: 500 Posts
- Posts: 111
- Joined: Sat Mar 07, 2015 11:00 pm
- Thanked: 8 times
- Followed by:1 members
Hi Mitch,GMATGuruNY wrote:The OA is not C but D.Max@Math Revolution wrote:There are 2 variables in the isosceles triangle and 1 in a square, so we need 3 variables in order to solve the problem.
There are only 2 equations given from the conditions, so there is high chance (E) will be our answer.
Looking at the conditions together, AC and AB passes through the midpoint of SE and QR, so the area of ABC is always greater that that of square SQRE, so this answers the question 'yes' and is sufficient.
The answer is (C).
In the figure above, SQRE is a square, AB = AC, and AS = AQ. What is the difference between the perimeter of triangle ABC and the perimeter of square SQRE?
(1) The length of RE is 4 times the length of BR.
(2) The area of triangle ABC is 75% of the area of square SQRE.
I think the question u have solved is different from the question posted. The figures look similar though.
Thanks.
- GMATGuruNY
- GMAT Instructor
- Posts: 15539
- Joined: Tue May 25, 2010 12:04 pm
- Location: New York, NY
- Thanked: 13060 times
- Followed by:1906 members
- GMAT Score:790
Good catch.binit wrote: Hi Mitch,
I think the question u have solved is different from the question posted. The figures look similar though.
Thanks.
I've amended my post accordingly.
Private tutor exclusively for the GMAT and GRE, with over 20 years of experience.
Followed here and elsewhere by over 1900 test-takers.
I have worked with students based in the US, Australia, Taiwan, China, Tajikistan, Kuwait, Saudi Arabia -- a long list of countries.
My students have been admitted to HBS, CBS, Tuck, Yale, Stern, Fuqua -- a long list of top programs.
As a tutor, I don't simply teach you how I would approach problems.
I unlock the best way for YOU to solve problems.
For more information, please email me (Mitch Hunt) at [email protected].
Student Review #1
Student Review #2
Student Review #3
Followed here and elsewhere by over 1900 test-takers.
I have worked with students based in the US, Australia, Taiwan, China, Tajikistan, Kuwait, Saudi Arabia -- a long list of countries.
My students have been admitted to HBS, CBS, Tuck, Yale, Stern, Fuqua -- a long list of top programs.
As a tutor, I don't simply teach you how I would approach problems.
I unlock the best way for YOU to solve problems.
For more information, please email me (Mitch Hunt) at [email protected].
Student Review #1
Student Review #2
Student Review #3