5-Day Free Trial
5-day free, full-access trial TTP
Available with Beat the GMAT members only code
MORE DETAILS
UPLOADED IMAGE_PS_Geometry
This topic has expert replies
-
gmat_thingie
- Junior | Next Rank: 30 Posts
- Posts: 23
- Joined: Thu Nov 12, 2009 12:37 am
GMAT/MBA Expert
-
[email protected]
- Elite Legendary Member
- Posts: 10392
- Joined: Sun Jun 23, 2013 6:38 pm
- Location: Palo Alto, CA
- Thanked: 2867 times
- Followed by:511 members
- GMAT Score:800
Hi gmat_thingie,
This prompt is incomplete - unless you include an actual LENGTH for ANY of the line segments, there's no way to determine the lengths of the other line segments.
GMAT assassins aren't born, they're made,
Rich
This prompt is incomplete - unless you include an actual LENGTH for ANY of the line segments, there's no way to determine the lengths of the other line segments.
GMAT assassins aren't born, they're made,
Rich
-
gmat_thingie
- Junior | Next Rank: 30 Posts
- Posts: 23
- Joined: Thu Nov 12, 2009 12:37 am
-
gmat_thingie
- Junior | Next Rank: 30 Posts
- Posts: 23
- Joined: Thu Nov 12, 2009 12:37 am
-
theCEO
- Master | Next Rank: 500 Posts
- Posts: 363
- Joined: Sun Oct 17, 2010 3:24 pm
- Thanked: 115 times
- Followed by:3 members
Two equations worthwhile to know:gmat_thingie wrote:Same question for "perimeter"
Sin 30 = 1/2
Sin 60 = sqrt(3)/2
lets label the point on CD where the two points meet as F
lets label the point on BC where the two points meet as E
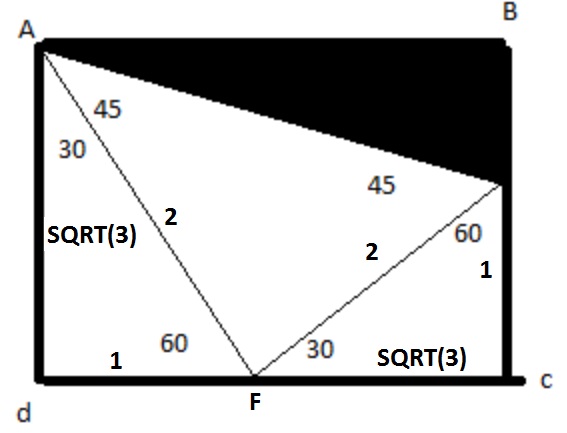
Area of reactangle = AD X CD
Area of reactangle = (sqrt 3) x (1 + sqrt 3) = sqrt 3 + 3
Area of trapezium = 1/2 * (AD + CE) * CD
Area of trapezium = 1/2 * (sqrt 3 + 1) * (1 + sqrt 3))
Area of trapezium = 1/2 * (3 + 2 * sqrt 3 + 1) = 1/2 * (4 + 2 * sqrt 3) = 2 + sqrt 3
Area of shaded region = (sqrt 3 + 3) - (2 + sqrt 3) = 1
Perimeter:
If we continue we have the following for the sides of the shaded region:
AB + BE + AE
1+sqrt(3) + (sqrt(3) - 1) + sqrt(2^2 + 2^2)
1+sqrt(3) + (sqrt(3) - 1) + 2sqrt2
2*sqrt(3) + 2sqrt2
