AAPL wrote:Manhattan Prep
The random variable x has the following continuous probability distribution in the range $$0 < x < \sqrt{2},$$ as shown in the coordinate plane with x on the horizontal axis:
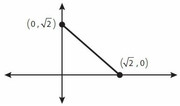
$$\text{The probability that } x < 0 = \text{ the probability that } x > \sqrt{2} = 0.$$
What is the median of x?
$$A.\ \frac{\sqrt{2}-1}{2} \,\,\,\, B.\ \frac{\sqrt{2}}{4} \,\,\,\,C.\ \sqrt{2}-1 \,\,\,\, D.\ \frac{\sqrt{2}+1}{4} \,\,\,\, E.\ \frac{\sqrt{2}}{2}$$
We are talking about the median of a continuous random variable with a given probability density function... and all this wording is absolutely out-of-GMAT´s-scope!
On the other hand, the same problem could be put into GMAT´s reality (for instance) like that:
In the figure above, what is the value of x such that the areas under the line from 0 to x, and from x to the square root of 2, coincide?

\[? = x\,\,\,\,:\,\,\,\,{S_{\,{\text{I}}}} + {S_{\,{\text{II}}}} = {S_{\,{\text{III}}}}\,\,\,\,\,\,\left( * \right)\]
\[{S_{\,{\text{I}}}} + {S_{\,{\text{II}}}} = \frac{{x \cdot x}}{2} + x\left( {\sqrt 2 - x} \right) = x\sqrt 2 - \frac{{{x^2}}}{2}\]
\[{S_{\,{\text{III}}}} = \frac{{\left( {\sqrt 2 - x} \right)\left( {\sqrt 2 - x} \right)}}{2} = \frac{{2 - 2x\sqrt 2 + {x^2}}}{2} = 1 + \frac{{{x^2}}}{2} - x\sqrt 2 \]
\[\left( * \right)\,\,\,\,\, \Rightarrow \,\,\,\,\,x\sqrt 2 - \frac{{{x^2}}}{2} = 1 + \frac{{{x^2}}}{2} - x\sqrt 2 \,\,\,\,\,\,\, \Rightarrow \,\,\,\,\,{x^2} - 2x\sqrt 2 + 1 = 0\]
\[{\text{Sum}}\,\, = \,\,\,2\sqrt 2 \,\,\,\,\,,\,\,\,\,{\text{Product}}\,\, = \,\,\,1\,\,\,\,\,\,\, \Rightarrow \,\,\,\,\,\,\,{x_1} = \sqrt 2 - 1\,\,,\,\,\,{x_2} = \sqrt 2 + 1\]
\[{x_2} > \sqrt 2 \,\,\,\,\,\, \Rightarrow \,\,\,\,\,? = {x_1} = \sqrt 2 - 1\]
The correct answer is therefore (C).
This solution follows the notations and rationale taught in the GMATH method.
Regards,
fskilnik.





















