(A) 7/3
(B) 4
(C) 5
(D) sqrt(7)
(E) sqrt(11)
For a set of Coordinate Geometry practice questions, including the OA and an OE with a diagram for this problem, see:
https://magoosh.com/gmat/2013/gmat-quan ... questions/
Mike
Circle passes through (0, 7) and (0, -1) and has centre on Y-axis which means that distance between (0, 7) and (0, -1) should be diameterMike@Magoosh wrote:The center of circle Q is on the y-axis, and the circle passes through points (0, 7) and (0, -1). Circle Q intersects the positive x-axis at (p, 0). What is the value of p?
(A) 7/3
(B) 4
(C) 5
(D) sqrt(7)
(E) sqrt(11)
For a set of Coordinate Geometry practice questions, including the OA and an OE with a diagram for this problem, see:
https://magoosh.com/gmat/2013/gmat-quan ... questions/
Mike
Sqrt(7) = 2.64Mathsbuddy wrote:Using the Equation of a Circle is certainly the right way to go.
However for speed, you could try this:
With a range from y = -1 to y = 7, it is easy to recognise that the radius is 4.
As the centre of the circle is not lying on the x-axis, it means that it must intersect the x-axis at a value less than 4. Ihis eliminates answers B and C straight away.
In fact, a very rough sketch shows that the x-intercepts have a magnitude just less than 3.
Only answer D complies with this.
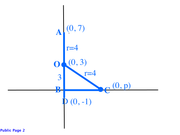
Nice one Mitch. Just a few typo errors in powers on the step [3³ + BC² = 4�]GMATGuruNY wrote:No special knowledge of circles is required here.
A quick drawing yields the following:
Since (0 -1,) and (0, 7) are both on the circle, AD is a diameter.
Thus, center O is located at (0, 3) -- halfway between (0, -1) and (0, 7) -- implying that r=4.
Since (0, p) is on the circle, OC is also a radius, implying that OC=4.
Since OB=3, and OB² + BC² = OC², we get:
3³ + BC² = 4�
BC² = 7
BC = √7.
Thus, p = √7.
The correct answer is D.
True! I forgot to dismiss this on the grounds that 7/3 = Sqrt(49/9), which containing a fraction, which could not exist in this case as all our rectilinear given dimensions are integer. (To be honest I did overlook this. Thanks)GMATinsight wrote:Sqrt(7) = 2.64Mathsbuddy wrote:Using the Equation of a Circle is certainly the right way to go.
However for speed, you could try this:
With a range from y = -1 to y = 7, it is easy to recognise that the radius is 4.
As the centre of the circle is not lying on the x-axis, it means that it must intersect the x-axis at a value less than 4. Ihis eliminates answers B and C straight away.
In fact, a very rough sketch shows that the x-intercepts have a magnitude just less than 3.
Only answer D complies with this.
7/3 = 2.33
Very precise approximation indeed...