Problem Solving

bobdylan wrote:If each term in the sum A1+A2+...An is either 7 or 77 and the sum equals 350, which of the following could be equal to n ?

a) 38
b) 39
c) 40
d) 41
e) 32

Looking for a pattern is one possible route:

Since both 7 and 77 have 7 as their units digit, we know that if we take any two terms, their sum will have a units digit of 4 (e.g., 7 + 7 = 14, 7 + 77 = 84, 77 + 77 = 154)

Similarly, if we take any three terms, their sum will have a units digit of 1. (e.g., 7 + 7 + 7 = 21, 7 + 7 + 77 = 91, etc.)

Now let's look for a pattern.

The sum of any 1 term will have units digit 7
The sum of any 2 terms will have units digit 4
The sum of any 3 terms will have units digit 1
The sum of any 4 terms will have units digit 8
The sum of any 5 terms will have units digit 5
The sum of any 6 terms will have units digit 2
The sum of any 7 terms will have units digit 9
The sum of any 8 terms will have units digit 6
The sum of any 9 terms will have units digit 3
The sum of any 10 terms will have units digit 0
The sum of any 11 terms will have units digit 7 (at this point, the pattern repeats)

From this, we can conclude that the sum of any 20 terms will have units digit 0
And the sum of any 30 terms will have units digit 0, and so on.

We are told the sum of the terms is 350 (units digit 0), so the number of terms must be 10 or 20 or 30 or . . .

Since C is a multiple of 10, this must be the correct answer.

Cheers,
Brent

Another option is to try some different configurations. If we do, we see that adding 39 7's and 1 77 gives us a total of 350. (39 + 1 = [spoiler]40 = C[/spoiler])

bobdylan wrote:If each term in the sum A1+A2+...An is either 7 or 77 and the sum equals 350, which of the following could be equal to n ?

a) 38
b) 39
c) 40
d) 41
e) 32

Hi bobdylan!

Another great way to solve this problem is to think about "hidden" constraints when you have only 1 equation and 2 variables to solve for. Here is what I mean...

If we know that some number of terms (let's say X of them) will equal 7, and some other number of terms (let's say Y of them) will equal 77, then I will be summing up x 7's and y 77's or 7x+77y and that sum will be 350, so 7x+77y=350. And we want to know what n is, right? Well n is the total number of terms, so we want to know what x+y=?

So we have one equation, 7x+77y=350 but 2 variables, so it would seem we couldn't solve for a specific x+y (and we're right, we can't), but because we know that x and y are both positive AND integers (hidden constraint based on the fact that x and y are both a number of terms), we can probably solve for a finite number of solutions. So let's see how that works...

First simplify as much as possible:
7x + 77y = 350
7(x + 11y) = 350
x + 11y = 50

Okay, now I like to make a table to identify the different possible values. Since the Y has the larger coefficient, it will have fewer possibilities to try (since 11 times 4 = 44 is the largest we can go without overshooting the sum of 50). We will want to list out the possible values of y, then from those we calculate the corresponding 11y and then the corresponding x values (which would equal 50-11y). Last we would want to quickly list the corresponding x+y values and see which are on our list:



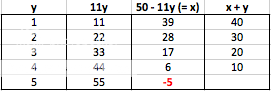
If we started with just y=1, we would have seen that we found an answer [spoiler](c)[/spoiler] and could stop, but I just finished the table for completeness sake! And again, see why anything larger than y=5 would not work - we get NEGATIVE values for X!!

Hope this helps - I use this "case listing" method for lots of problems (particularly DS) when you have a single equation, 2 unknowns BUT some hidden integer constraints!!


Whit