Data Sufficiency

koby_gen wrote:Is ( 7^(X+2) ) / 49 > 1 ?

(1) 7^(x+2) > 1/49
(2) 7^(x-1) > 1/49

.... 7^(x + 2)/49 > 1
=> 7^(x + 2) > 49 = 7^2
=> (x + 2) > 2
=> x > 0

Hence, the problems is asking whether x is greater than 0 or not.

Statement 1: 7^(x + 2) > 1/49 = 7^(-2)
Implies, (x + 2) > -2
=> x > -4

Not sufficient


Statement 2: 7^(x - 1) > 1/49 = 7^(-2)
Implies, (x - 1) > -2
=> x > -1

Not sufficient

1 & 2 Together: x > -1

Not sufficient.

The correct answer is E.

Anurag@Gurome wrote:

koby_gen wrote:Is ( 7^(X+2) ) / 49 > 1 ?

(1) 7^(x+2) > 1/49
(2) 7^(x-1) > 1/49

.... 7^(x + 2)/49 > 1
=> 7^(x + 2) > 49 = 7^2
=> (x + 2) > 2
=> x > 2

Hence, the problems is asking whether x is greater than 2 or not.

Quick note - simplifying (x+2)>2, the question rephrase should be "is x>0"? In this problem it does not change the end result however.

A question for the OP - what is the source of this question? It tests solid theory but the set-up seems a bit off for the GMAT.

Thanks!
Whit

Whitney Garner wrote:Quick note - simplifying (x+2)>2, the question rephrase should be "is x>0"?

Thanks Whitney.
Edited the reply.

Night reader wrote:rather hesitating to post this one ...

( 7^(X+2) ) / 49 > 1 ---> 7^(x+2)>|7|^2 ? can not be further simplified

It actually can be simplified further. If we leave everything on the left side we can investigate the 2 cases that seem to arise from |7|^2. We'll start with the positive case:



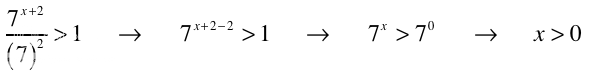
Now, the negative case. We will have to use the fact that (-7)^2 = (-1 * 7)^2



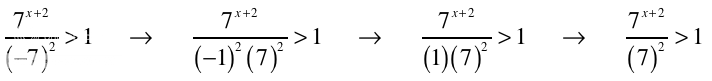
and we find ourselves exactly where we were in the positive case. So in either case we will have the same simplification. Another way is to break up that numerator and not even bother with factoring 49:



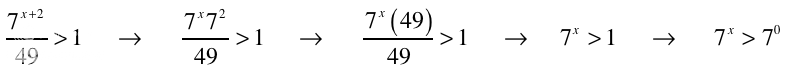
And again, we're back to x>0.

But we can think about it more conceptually. In order for that fraction to be greater than 1, the numerator needs to be larger than the denominator (because they are both positive). That all hinges on what happens with X. If X is anything positive, then the numerator is going to be something greater than 49 divided by 49 is greater than 1. But if X is anything negative, then the numerator is something less than 7^2 or less than 49, so the fraction is less than 1.

**The beauty of many exponential equations is that there are a half-dozen ways to get at an answer, so we can sit back, relax and just start trying things

I hope this helps!

Whit

Night reader wrote:Whit, (7^x)*49 in the numerator and 49 in the denominator are two different numbers in the mods
one is 7^2 from original source number, and the other is 49 - we don't know the original number

further to equate the powers one needs to have the same baseline number on both sides (left and right)
we have +ve 7 on the left and -ve 7 on the right in case when |7|=-7
So when I said can't be further simplified, it was meant that this expression breaks down to two expressions exactly:

7^(x+2)>|7|^2 AND |7|>7 {+ve} --> 7^(x+2)>7^2 This we can simplify and write as x+2>2
7^(x+2)>|7|^2 AND |7|>-7 {-ve} --> 7^(x+2)>-7^2 Here we can't write as x+2>2 because the baseline numbers are of the different values 7 and -7

OR in the more straightforward way

7^(x+2)/|7|^2 >1 --> for |7| -ve, 7^(x+2)<-7^2 AND for |7| +ve, 7^(x+2)>7^2 ... actually this would be the correct way, as we can not multiply inequality to the mod. What do you think?

49/49 will be 1 regardless of the underlying values used to create those 49s. To put this in a slightly different perspective - if I asked you for 81/81, you would not have to first ask if one was 9^2 and the other (-9)^2 or answer +1 or -1; the answer would simply be 1. If the numerator was made of (-9)(-9) and the denominator by (9)(9), the answer would only be 1 because the negatives will be paired and will cancel. We only have to worry about the mod or underlying sign of 7 if we are trying to pull out only one of the 7s in the denominator - but we are treating them as a whole. We can think about it in the following way:

(-7)*(-7) = (7)*(7)
(-7)^2 = 7^2
49 = 49

At every step of the expression we are equal. We would only need to be concerned with these "hidden" signs if we decided to remove one of the terms (i.e. take the square root). Because we do not have to do that to solve the problem asked in the post, we are home free.

In the step you noted here:

Night reader wrote:7^(x+2)>|7|^2 AND |7|>-7 {-ve} --> 7^(x+2)>-7^2 Here we can't write as x+2>2 because the baseline numbers are of the different values 7 and -7

Be careful, because I can rewrite (-7)^2 as (-1)^2 times (7)^2 and this is a legal move. And since (-1)^2 = 1, that term effectively disappears.

Again, 3 different methods will get you to the same solution, x>0, and only one of them utilizes "factoring" of the 49 in the denominator.


Whit