In how many ways can 4 ladies and 5 gentlemen be seated in a row so that no two ladies sit together?
A. 43200
B. 21600
C. 5760
D. 2880
E. 1440
[spoiler]OA A[/spoiler]
www.manyagroup.org
no two ladies sit together?
This topic has expert replies
- sanju09
- GMAT Instructor
- Posts: 3650
- Joined: Wed Jan 21, 2009 4:27 am
- Location: India
- Thanked: 267 times
- Followed by:80 members
- GMAT Score:760
The mind is everything. What you think you become. -Lord Buddha
Sanjeev K Saxena
Quantitative Instructor
The Princeton Review - Manya Abroad
Lucknow-226001
www.manyagroup.com
Sanjeev K Saxena
Quantitative Instructor
The Princeton Review - Manya Abroad
Lucknow-226001
www.manyagroup.com
GMAT/MBA Expert
- Brent@GMATPrepNow
- GMAT Instructor
- Posts: 16207
- Joined: Mon Dec 08, 2008 6:26 pm
- Location: Vancouver, BC
- Thanked: 5254 times
- Followed by:1268 members
- GMAT Score:770
Take the task of seating everyone and break it into stages.sanju09 wrote:In how many ways can 4 ladies and 5 gentlemen be seated in a row so that no two ladies sit together?
A. 43200
B. 21600
C. 5760
D. 2880
E. 1440
Stage 1: Arrange all of the men in a row
We can arrange k unique objects in k! ways.
Since there are 5 men, we can arrange them in 5! (120 ways)
IMPORTANT: Now place an empty chair on either side of each man as follows:
_M_M_M_M_M_
Note: This prevents the women from sitting together because there is now a man separating each of 6 empty chairs.
Stage 2: Seat a woman
There are 6 seats, so we can complete this stage in 6 ways
Stage 3: Seat another woman
There are 5 seats remaining, so we can complete this stage in 5 ways
Stage 4: Seat another woman
There are 4 seats remaining, so we can complete this stage in 4 ways
Stage 5: Seat the last woman
There are 3 seats remaining, so we can complete this stage in 3 ways
By the Fundamental Counting Principle (FCP), we can complete all 5 stages (and thus seat all 9 people) in (120)(6)(5)(4)(3) ways ([spoiler]= 43200, ways[/spoiler])
Answer: A
Here's a similar question to practice with: https://www.beatthegmat.com/p-c-pls-help-t29328.html
Cheers,
Brent
Aside: For more information about the FCP, watch our free video: https://www.gmatprepnow.com/module/gmat-counting?id=775
- Quasar Chunawala
- Newbie | Next Rank: 10 Posts
- Posts: 7
- Joined: Wed Apr 16, 2014 9:41 pm
- Thanked: 4 times
The explanation above is extremely clear. It helps if you remember permutations and combinations from college-time.
The number of ways of arranging r objects from a set of n items are
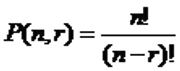
The number of ways of selecting r objects from n choices are
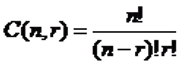
You can arrange 5 gentlemen in P(5,5) = 5! = 120 ways
_M_M_M_M_M_
Further, you can arrange 4 women in the 6 empty slots in P(6,4) = 6!/2! = 360 ways
So, number of ways you can do this = (120)(360) = 43,200 ways
The number of ways of arranging r objects from a set of n items are
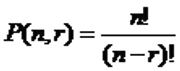
The number of ways of selecting r objects from n choices are
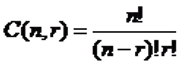
You can arrange 5 gentlemen in P(5,5) = 5! = 120 ways
_M_M_M_M_M_
Further, you can arrange 4 women in the 6 empty slots in P(6,4) = 6!/2! = 360 ways
So, number of ways you can do this = (120)(360) = 43,200 ways
-
nikhilgmat31
- Legendary Member
- Posts: 518
- Joined: Tue May 12, 2015 8:25 pm
- Thanked: 10 times
Hi Brent,
Counting the number of way for 5 Men = 120 seems fine.
But Why can't we have a pattern of 4 women as M_M_M_M_M
where we will have 4 * 3 * 2 * 1 = 24 options for ladies.
total of 120* 24 = 2880 options.
Also can't we solve this question using other formula as - 9!/(5!*4!) = 126 .....
Counting the number of way for 5 Men = 120 seems fine.
But Why can't we have a pattern of 4 women as M_M_M_M_M
where we will have 4 * 3 * 2 * 1 = 24 options for ladies.
total of 120* 24 = 2880 options.
Also can't we solve this question using other formula as - 9!/(5!*4!) = 126 .....
GMAT/MBA Expert
- Brent@GMATPrepNow
- GMAT Instructor
- Posts: 16207
- Joined: Mon Dec 08, 2008 6:26 pm
- Location: Vancouver, BC
- Thanked: 5254 times
- Followed by:1268 members
- GMAT Score:770
The pattern you describe (M_M_M_M_M) is already included in my solution.nikhilgmat31 wrote:Hi Brent,
Counting the number of way for 5 Men = 120 seems fine.
But Why can't we have a pattern of 4 women as M_M_M_M_M
where we will have 4 * 3 * 2 * 1 = 24 options for ladies.
total of 120* 24 = 2880 options.
Also can't we solve this question using other formula as - 9!/(5!*4!) = 126 .....
We can use your pattern but we must recognize that we still need to examine other patterns (like MM_M_M_M_ and _M_MM_M_M) if want to count ALL possibilities.
My solution considers all possibilities.
This formula finds the number of ways to select 5 seats from 9 seats. It does not adhere to the restriction that no two women can sit together.Also can't we solve this question using other formula as - 9!/(5!*4!) = 126 .....
Cheers,
Brent
-
nikhilgmat31
- Legendary Member
- Posts: 518
- Joined: Tue May 12, 2015 8:25 pm
- Thanked: 10 times
Yes Brent,Brent@GMATPrepNow wrote:The pattern you describe (M_M_M_M_M) is already included in my solution.nikhilgmat31 wrote:Hi Brent,
Counting the number of way for 5 Men = 120 seems fine.
But Why can't we have a pattern of 4 women as M_M_M_M_M
where we will have 4 * 3 * 2 * 1 = 24 options for ladies.
total of 120* 24 = 2880 options.
Also can't we solve this question using other formula as - 9!/(5!*4!) = 126 .....
We can use your pattern but we must recognize that we still need to examine other patterns (like MM_M_M_M_ and _M_MM_M_M) if want to count ALL possibilities.
My solution considers all possibilities.
This formula finds the number of ways to select 5 seats from 9 seats. It does not adhere to the restriction that no two women can sit together.Also can't we solve this question using other formula as - 9!/(5!*4!) = 126 .....
Cheers,
Brent
I still didn't get how your solution all the patterns like _M_M_M_M_M_ or M_M_M_M_M or _MM_M_M_M or MM_M_M_M_ or _M_MM_M_M.
Please help me understand.
GMAT/MBA Expert
- Brent@GMATPrepNow
- GMAT Instructor
- Posts: 16207
- Joined: Mon Dec 08, 2008 6:26 pm
- Location: Vancouver, BC
- Thanked: 5254 times
- Followed by:1268 members
- GMAT Score:770
In the scenario _M_M_M_M_M_ we can place the 4 women in ANY of the 6 spaces and we will meet the restriction that no 2 women can sit together.nikhilgmat31 wrote:Yes Brent,Brent@GMATPrepNow wrote:The pattern you describe (M_M_M_M_M) is already included in my solution.nikhilgmat31 wrote:Hi Brent,
Counting the number of way for 5 Men = 120 seems fine.
But Why can't we have a pattern of 4 women as M_M_M_M_M
where we will have 4 * 3 * 2 * 1 = 24 options for ladies.
total of 120* 24 = 2880 options.
Also can't we solve this question using other formula as - 9!/(5!*4!) = 126 .....
We can use your pattern but we must recognize that we still need to examine other patterns (like MM_M_M_M_ and _M_MM_M_M) if want to count ALL possibilities.
My solution considers all possibilities.
This formula finds the number of ways to select 5 seats from 9 seats. It does not adhere to the restriction that no two women can sit together.Also can't we solve this question using other formula as - 9!/(5!*4!) = 126 .....
Cheers,
Brent
I still didn't get how your solution all the patterns like _M_M_M_M_M_ or M_M_M_M_M or _MM_M_M_M or MM_M_M_M_ or _M_MM_M_M.
Please help me understand.
Cheers,
Brent
- sanju09
- GMAT Instructor
- Posts: 3650
- Joined: Wed Jan 21, 2009 4:27 am
- Location: India
- Thanked: 267 times
- Followed by:80 members
- GMAT Score:760
Such a great explanation, Brent! Nothing is clearer than this, it's just just treat to watch. It's simply a practical and methodical approach to such problems, where formulaic approaches such as 9!/(5!*4!) = 126 ..... could make one confused whether it's a Permutation case or what? Formulaic approaches on most of the GMAT Math Problems on the real test such as this could take one to the wrong side of the road. Hence we should rely more on methodical, innovative, and practical approaches on hard problems in particular rather than looking for any magic stick. Majestic
The mind is everything. What you think you become. -Lord Buddha
Sanjeev K Saxena
Quantitative Instructor
The Princeton Review - Manya Abroad
Lucknow-226001
www.manyagroup.com
Sanjeev K Saxena
Quantitative Instructor
The Princeton Review - Manya Abroad
Lucknow-226001
www.manyagroup.com
Brent why we have stopped with (120)(6)(5)(4)(3) and not included another 2 ways .Brent@GMATPrepNow wrote:Take the task of seating everyone and break it into stages.sanju09 wrote:In how many ways can 4 ladies and 5 gentlemen be seated in a row so that no two ladies sit together?
A. 43200
B. 21600
C. 5760
D. 2880
E. 1440
Stage 1: Arrange all of the men in a row
We can arrange k unique objects in k! ways.
Since there are 5 men, we can arrange them in 5! (120 ways)
IMPORTANT: Now place an empty chair on either side of each man as follows:
_M_M_M_M_M_
Note: This prevents the women from sitting together because there is now a man separating each of 6 empty chairs.
Stage 2: Seat a woman
There are 6 seats, so we can complete this stage in 6 ways
Stage 3: Seat another woman
There are 5 seats remaining, so we can complete this stage in 5 ways
Stage 4: Seat another woman
There are 4 seats remaining, so we can complete this stage in 4 ways
Stage 5: Seat the last woman
There are 3 seats remaining, so we can complete this stage in 3 ways
By the Fundamental Counting Principle (FCP), we can complete all 5 stages (and thus seat all 9 people) in (120)(6)(5)(4)(3) ways ([spoiler]= 43200, ways[/spoiler])
Answer: A
Here's a similar question to practice with: https://www.beatthegmat.com/p-c-pls-help-t29328.html
Cheers,
Brent
Aside: For more information about the FCP, watch our free video: https://www.gmatprepnow.com/module/gmat-counting?id=775
What I mean is (120)(6)(5)(4)(3)(2)
GMAT/MBA Expert
- Brent@GMATPrepNow
- GMAT Instructor
- Posts: 16207
- Joined: Mon Dec 08, 2008 6:26 pm
- Location: Vancouver, BC
- Thanked: 5254 times
- Followed by:1268 members
- GMAT Score:770
By the time we complete stage 5, we have seated all of the people. So, we have completed our task of seating everyone.ash4gmat wrote:Brent why we have stopped with (120)(6)(5)(4)(3) and not included another 2 ways .Brent@GMATPrepNow wrote:Take the task of seating everyone and break it into stages.sanju09 wrote:In how many ways can 4 ladies and 5 gentlemen be seated in a row so that no two ladies sit together?
A. 43200
B. 21600
C. 5760
D. 2880
E. 1440
Stage 1: Arrange all of the men in a row
We can arrange k unique objects in k! ways.
Since there are 5 men, we can arrange them in 5! (120 ways)
IMPORTANT: Now place an empty chair on either side of each man as follows:
_M_M_M_M_M_
Note: This prevents the women from sitting together because there is now a man separating each of 6 empty chairs.
Stage 2: Seat a woman
There are 6 seats, so we can complete this stage in 6 ways
Stage 3: Seat another woman
There are 5 seats remaining, so we can complete this stage in 5 ways
Stage 4: Seat another woman
There are 4 seats remaining, so we can complete this stage in 4 ways
Stage 5: Seat the last woman
There are 3 seats remaining, so we can complete this stage in 3 ways
By the Fundamental Counting Principle (FCP), we can complete all 5 stages (and thus seat all 9 people) in (120)(6)(5)(4)(3) ways ([spoiler]= 43200, ways[/spoiler])
Answer: A
Here's a similar question to practice with: https://www.beatthegmat.com/p-c-pls-help-t29328.html
Cheers,
Brent
Aside: For more information about the FCP, watch our free video: https://www.gmatprepnow.com/module/gmat-counting?id=775
What I mean is (120)(6)(5)(4)(3)(2)
Cheers,
Brent




















