Data Sufficiency

Hi,
Basic knowledge of slopes and intercepts of line is required to solve this question.
Remember: We can always draw and visualize and co-ordinate geometry question to solve it faster.
Given: Line K has negative slope,
If the line k is not passing through the origin and has negative slope then the intercepts will have same signs.
You can draw and visualize the lines to understand it better.
Statement I is insufficient:
The x-intercept of line k is less than the y-intercept of line k.
We cant say whether line k has positive y-intercept with this statement.
For example, if line k has intercept points as (0,4) and (2,0) where Y-intercept is greater than the X-intercept. So answer to the question would be YES here.
But if line k has intercept point as (-4,0) and (0,-2), where Y-intercept is greater than the X-intercept. But answer to the question would be NO here.
Statement II is insufficient:
The slope of line k is less than -2.
We can take the same above example here for YES answer, Where the slope is negative 2 and answer to the question is YES.
But answer to the question would be NO too.
For example, if the line passes through the origin, then both the intercepts are zero.
Lets say the line is y = -2x,
Where slope is -2, but the y-intercept is not positive.
So not sufficient.
Both statement together are sufficient,
Since x-intercept of line k is less than the y-intercept of line k and also slope is negative 2 only way to achieve this is if both the intercepts are positive. Hence Y intercept is positive
So, the answer is C. Together sufficient.

BTGmoderatorDC wrote:In the xy-plane, if line k has negative slope, is the y-intercept of line k positive?

(1) The x-intercept of line k is less than the y-intercept of line k.

(2) The slope of line k is less than -2.

Source: Veritas Prep

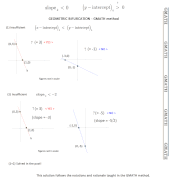
In the image attached, we have proved that each statement alone is insufficient through GEOMETRIC BIFURCATIONS.

\[\left( {1 + 2} \right)\,\]
\[{x_{\,k}}\,\, = \,\,{\left( {x - {\text{intercept}}} \right)_{\,k}}\]
\[{y_{\,k}}\,\, = \,\,{\left( {y - {\text{intercept}}} \right)_{\,k}}\,\,\]
\[{\text{slop}}{{\text{e}}_{\,k}}\,\,\, < \,\,\,\,0\]
\[{y_{\,k}}\,\,\mathop > \limits^? \,\,\,0\]
\[\underline {{x_k} = 0} \,\,\,\,\,\mathop \Rightarrow \limits^{\left( 1 \right)} \,\,\,\,\left\{ \begin{gathered}
{y_k} > 0 \hfill \\
{\text{slop}}{{\text{e}}_{\,k}}\,\,\, < \,\,\,\,0 \hfill \\
\end{gathered} \right.\,\,\,\,\,\,\, \Rightarrow \,\,\,\,\underline {{x_k} > 0} \,\,\,\,\,\,{\text{impossible}}\,\,\,\,\,\,\, \Rightarrow \,\,\,\,\,\,{x_k} \ne 0\]
\[\left( {{x_k} \ne 0} \right)\,\,\,\,\, - \frac{{{y_{\,k}}}}{{{x_{\,k}}}}\,\, = \,\,\,\frac{{{y_{\,k}} - 0}}{{0 - {x_{\,k}}\,}}\,\,\,{\text{ = }}\,\,\,\,{\text{slop}}{{\text{e}}_{\,k}}\,\,\,\left\{ \begin{gathered}
< \,\,\,\,0\,\,\,\,\,\,\,\, \Rightarrow \,\,\,\,\,\,\,{y_k}\,\,,\,\,{x_k}\,\,{\text{same}}\,\,{\text{signs}}\,\,\,\,\,\left( {{\text{both}}\,\, \ne 0\,\,} \right)\,\,\,\,\,\,\,\,\left( * \right) \hfill \\
\mathop < \limits^{\left( 2 \right)} - 2\,\,\,\,\,\,\,\, \Rightarrow \,\,\,\,\,\, - \frac{{{y_{\,k}}}}{{{x_{\,k}}}} < - 2\,\,\,\,\,\,\, \Rightarrow \,\,\,\,\,\,\frac{{{y_{\,k}}}}{{{x_{\,k}}}} > 2\,\,\,\,\,\,\,\,\,\left( {**} \right)\, \hfill \\
\end{gathered} \right.\]
\[\underline {{y_k} < 0} \,\,\,\,\,\,\mathop \Rightarrow \limits^{\left( * \right)} \,\,\,\,\,{x_k} < 0\,\,\,\,\,\,\mathop \Rightarrow \limits^{\left( {**} \right)} \,\,\,\,\,\,{y_{\,k}} < \,\,\,2\,\,{x_{\,k}}\,\,\,\mathop < \limits^{{x_k}\,\, < \,\,0} \,\,\,{x_k}\,\,\,\,\,\, \Rightarrow \,\,\,\,\,\,\underline {\,\left( 1 \right)\,\,\,{\text{contradicted}}\,} \]
\[\left. \begin{gathered}
{y_k} < 0\,\,\,{\text{false}}\,\,\, \hfill \\
{y_k}\,\, \ne 0\,\,\,\,\left( * \right) \hfill \\
\end{gathered} \right\}\,\,\,\,\, \Rightarrow \,\,\,\,{y_k} > 0\,\,\,\,\, \Rightarrow \,\,\,\,\,\left\langle {{\text{YES}}} \right\rangle \,\,\,\,\, \Rightarrow \,\,\,\,\,{\text{SUFF}}.\]

This solution follows the notations and rationale taught in the GMATH method.

Regards,
Fabio.