Target Test Prep's 2024 GMAT Focus Edition prep is discounted for the BTG community!

Redeem
Target Test Prep
5-Day Free Trial
5-day free, full-access trial TTP

Available with Beat the GMAT members only code

MORE DETAILS
Target Test Prep
Magoosh
Magoosh
Study with Magoosh GMAT prep

Available with Beat the GMAT members only code

MORE DETAILS
Magoosh

If the triangle ABC is inscribed in semi-circle BAC as above

This topic has expert replies
Post new topic Post Reply
Previous Topic Next Topic
User avatar
Elite Legendary Member
Posts: 3991
Joined: Fri Jul 24, 2015 2:28 am
Location: Las Vegas, USA
Thanked: 19 times
Followed by:37 members

If the triangle ABC is inscribed in semi-circle BAC as above

by Max@Math Revolution » Sun Mar 06, 2016 4:01 pm
Image

If the triangle ABC is inscribed in semi-circle BAC as above figure and BC is a diameter, the length of AB is 6 and the length of AC is 8, what is the length of arc BAC?

A. 5Ï€(pi)
B. 6Ï€(pi)
C. 7Ï€(pi)
D. 8Ï€(pi)
E. 10 π(pi)


* A solution will be posted in two days.
Top

GMAT/MBA Expert

User avatar
GMAT Instructor
Posts: 16207
Joined: Mon Dec 08, 2008 6:26 pm
Location: Vancouver, BC
Thanked: 5254 times
Followed by:1268 members
GMAT Score:770

If the triangle ABC is inscribed in semi-circle BAC as above

by Brent@GMATPrepNow » Mon Mar 07, 2016 11:22 am
Max@Math Revolution wrote: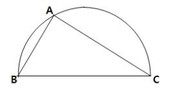Image

If the triangle ABC is inscribed in semi-circle BAC as above figure and BC is a diameter, the length of AB is 6 and the length of AC is 8, what is the length of arc BAC?

A. 5Ï€
B. 6Ï€
C. 7Ï€
D. 8Ï€
E. 10Ï€
Since BC is the diameter of the semi-circle, we know that ∠BAC is 90º
For more on this circle property, watch this free video - https://www.gmatprepnow.com/module/gmat ... /video/880

In other words, we can conclude that BAC is a RIGHT TRIANGLE and side BC is the HYPOTENUSE.
This means we can apply the Pythagorean Theorem to get: 6² + 8² = (side BC)²
Simplify: 36 + 64 = (side BC)²
Simplify: 100 = (side BC)²
So, side BC = 10
In other words, the DIAMETER = 10

Circumference of COMPLETE circle = (DIAMETER)(Ï€)
So, circumference of SEMIcircle = (DIAMETER)(Ï€)/2
= (10)(Ï€)/2
= 5Ï€

Answer: A

Cheers,
Brent
Last edited by Brent@GMATPrepNow on Mon Apr 30, 2018 8:59 am, edited 2 times in total.
Brent Hanneson - Creator of GMATPrepNow.com
Image
Top
User avatar
Elite Legendary Member
Posts: 3991
Joined: Fri Jul 24, 2015 2:28 am
Location: Las Vegas, USA
Thanked: 19 times
Followed by:37 members

by Max@Math Revolution » Tue Mar 08, 2016 4:03 pm
If the triangle ABC is inscribed in semi-circle BAC as above figure and BC is a diameter, the length of AB is 6 and the length of AC is 8, what is the length of arc BAC?

A. 5Ï€(pi)
B. 6Ï€(pi)
C. 7Ï€(pi)
D. 8Ï€(pi)
E. 10 π(pi)


->Since BC is a diameter, angle A is 90 degrees. According to Pythagoras' theorem, AB^2+AC^2=BC^2 -> 6^2+8^2=10^2 and BC=10. Then, a circumference with a diameter 10 is 10Ï€(pi). The question asks arc BAC, which is 10Ï€/2=5Ï€. Thus, A is the answer.
Top
Newbie | Next Rank: 10 Posts
Posts: 9
Joined: Tue Nov 17, 2015 7:22 pm
Thanked: 1 times

by rdds » Thu Mar 10, 2016 12:27 am
Angle A = 90 degree also it is a 3,4,5 triangle
so diameter is 10, r = 10/2 = 5
Circumference of a circle = 2 pi * r
semi-circle = pi*r= 5*pi
Answer : A
Top
Post new topic Post Reply
• Page 1 of 1