BREAKING: Target Test Prep releases Brand New 2026 On Demand GMAT prep course
Redeem
Featured Course
Scott Woodbury-Stewart’s private virtual classroom — 400 hours of master-class video lessons for the GMAT Focus Edition.
Target question: What percent of the area of rectangle ABCD is covered by the tiles?sidceg wrote:
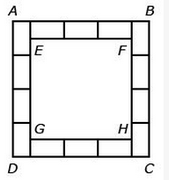
In the diagram, the fourteen rectangular tiles are all identical. What percent of the area of rectangle ABCD is covered by the tiles?
(1) ABCD is a square.
(2) EFGH is a square.
Jim@StratusPrep wrote:The answer here is D.
Whether you are looking at square ABCD or EFGH you can see that the length and height of the outer rectangles must be the same. So horizontally, 3 rectangles and 2 half rectangles equals the vertical height of 4 rectangles. Because the 2 half rectangles equal the one rectangle, they must all be the same.
Wow! Thank you so much Jim and Brent. I straight away thought without knowing the sides or at least the ratio of the sides of the two squares, the question cannot be solved. But the logic 4L = 3L + 2W did not strike my mind.Brent@GMATPrepNow wrote:
Target question: What percent of the area of rectangle ABCD is covered by the tiles?
Statement 1: ABCD is a square
IMPORTANT: Once we know that ABCD is a square, we also know that EFGH is a square. Notice that if you take square ABCD and "shave" off the same amount (i.e., the width of each rectangle) from the four sides, we get another square (EFGH).
Let L = length of one rectangle.
Side AD has length 4L, which means all four sides of square ABCD have length 4L.
So, the area of ABCD = (4L)(4L) = 16L^2
Side EF has length 3L, which means all four sides of square EFGH have length 3L.
So, the area of EFGH = (3L)(3L) = 9L^2
From this, we can conclude that the total area of the rectangles = 16L^2 - 9L^2 = 7L^2
So, the fraction of square ABCD taken up by tiles = (7L^2)/(16L^2) = 7/16
Since we could convert 7/16 to a percent, we could determine the percent of the area of rectangle ABCD is covered by the tiles.
Since we can answer the target question with certainty, statement 1 is SUFFICIENT
Statement 2: EFGH is a square
Using the same logic that we used above, we know that ABCD must also be a square.
From here, if we follow the same steps as above, we can answer the target question with certainty.
So statement 2 is SUFFICIENT
Answer = D
Cheers,
Brent
New here Create free account
