Problem Solving

In the coordinate plane, a circle has center (2, -3) and passes through the point (5, 0). What is the area of the circle?

A. 3Ï€
B. 3√2π
C. 3√3π
D. 9Ï€
E. 18Ï€

Can anyone say what are the concepts that it is testing?
How to relate coordinate geometry with circles?

komati_anusha wrote:In the coordinate plane, a circle has center (2, -3) and passes through the point (5, 0). What is the area of the circle?

A. 3Ï€
B. 3√2π
C. 3√3π
D. 9Ï€
E. 18Ï€

When given a shape on the coordinate plane, use the coordinate plane to learn about the shape, use the shape to learn about the coordinate plane, or do both.

Here, we can use the coordinate plane to learn about the circle.
DRAW:

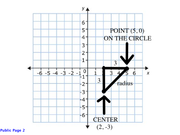
As the figure above shows, the radius of the circle is the hypotenuse of an isosceles right triangle with legs of length 3.
In an isosceles right triangle, the sides are in the following ratio:
x : x : x√2.
Thus, the sides of the isosceles right triangle in the figure above are 3 : 3 : 3√2, implying that the radius of the circle = 3√2.
Since A = πr², we get:
A = π(3√2)² = 18π.

The correct answer is E.

In the coordinate plane, a circle has center (2, -3) and passes through the point (5, 0). What is the area of the circle?
The displacement between points (2,-3) and (5,0) is the radius of the circle.
Change in x = 5 - 2 = 3
Change in y = 0 - -3 = 3
By Pythagoras: r^2 = 3^2 + 3^2 = 18
Area = pi x r^2 = 18 x pi

Hi Mitch Hunt!

I understood
But radius of a circle is the hypotenuse of a isosceles triangle.
But in a circle , radius will be same from center to any point in a circle.
And why can't we consider legs of a triangle as a radius in this.

sorry for silly questions!Pls

komati_anusha wrote:Hi Mitch Hunt!

I understood
But radius of a circle is the hypotenuse of a isosceles triangle.
But in a circle , radius will be same from center to any point in a circle.
And why can't we consider legs of a triangle as a radius in this.

sorry for silly questions!Pls

The hypotenuse is a radius because it extends from the center (2, -3) to a point on the circle (5, 0).
As shown in my solution above, the hypotenuse -- and thus the radius -- each have a length of 3√2.
All radii in a circle have the same length.
Since the legs of the triangle each have a length of 3, and the radius has a length of 3√2, the legs of the triangle cannot be radii.