BREAKING: Target Test Prep releases Brand New 2026 On Demand GMAT prep course

Redeem
TTP OnDemand GMAT Video Course
Featured Course

Target Test Prep GMAT OnDemand

Scott Woodbury-Stewart’s private virtual classroom — 400 hours of master-class video lessons for the GMAT Focus Edition.

  • 715+ score guarantee — highest in the industry (99th percentile)
  • 52 chapters · 1,500+ lessons · 4,000+ practice questions
  • 400 hours of video · 1,500+ instructor-led HD smartboard lessons
  • 300,000+ students accepted to Harvard, Stanford, Wharton, Booth & Sloan & more
  • 24/7 live support + weekly Zoom office hours with GMAT instructors
  • TTP AI Assist — 24/7 AI-powered virtual tutor for instant help
  • 1,200+ flashcards + AI-powered study assistant & daily calendar
  • OnDemand, LiveTeach & GMAT Bootcamp formats available
  • Also: GRE, SAT Math & Executive Assessment courses
  • MBA Admissions Consulting now available
  • 🏆 2025 EdTech Breakthrough Award: Test Prep Solution Provider of the Year
  • 200,000+ students served
  • 5-day free trial — $0 to start, no auto-billing, cancel anytime
★★★★★ 5.0 (559 reviews)
130-pt guarantee
$0 to start then $127/mo
Start Free 5-Day Trial Read 559 Reviews →

Geometry

Expert replies
Post new topic Post Reply
Previous Topic Next Topic
Senior | Next Rank: 100 Posts
Posts: 98
Joined: Sat May 31, 2014 8:29 pmFollowed by: 2 members
Thanked: 1 times
by RiyaR » Sun Oct 05, 2014 3:58 am
A circle with a radius of 4 has an equilateral traingle inscribed in it. What is the perimeter of the inscribed equilateral triangle?

A) 6 root 2
B) 6 root 3
C) 12 root 3
D) 12 root2
E) 24
Top
Join the discussion
Log in to postLogin with Googleuse password
QUOTE IN REPLY
Source: — Problem Solving |
User avatar
GMAT Instructor
Posts: 15539
Joined: Tue May 25, 2010 12:04 pmFollowed by: 1906 members
Location: New York, NY
Thanked: 13060 times
GMAT Score:790

by GMATGuruNY » Sun Oct 05, 2014 4:08 am
Check my posts below:

Ballparking method:
https://www.beatthegmat.com/ps-triangle-t98932.html (2 posts)
Alternate method:
https://www.beatthegmat.com/difficult-ge ... 95817.html
Private tutor exclusively for the GMAT and GRE, with over 20 years of experience.
Followed here and elsewhere by over 1900 test-takers.
I have worked with students based in the US, Australia, Taiwan, China, Tajikistan, Kuwait, Saudi Arabia -- a long list of countries.
My students have been admitted to HBS, CBS, Tuck, Yale, Stern, Fuqua -- a long list of top programs.

As a tutor, I don't simply teach you how I would approach problems.
I unlock the best way for YOU to solve problems.

For more information, please email me (Mitch Hunt) at [email protected].
Student Review #1
Student Review #2
Student Review #3
Top
Join the discussion
Log in to postLogin with Googleuse password
QUOTE IN REPLY

GMAT/MBA Expert

User avatar
GMAT Instructor
Posts: 16207
Joined: Mon Dec 08, 2008 6:26 pmFollowed by: 1268 members
Location: Vancouver, BC
Thanked: 5254 times
GMAT Score:770

Geometry

by Brent@GMATPrepNow » Sun Oct 05, 2014 7:39 am
RiyaR wrote:A circle with a radius of 4 has an equilateral triangle inscribed in it. What is the perimeter of the inscribed equilateral triangle?

A) 6√2
B) 6√3
C) 12√3
D) 12√2
E) 24
So, here's what the diagram looks like.
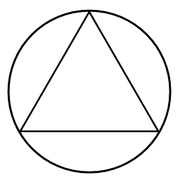
Image

If we draw lines from the center to each vertex, we get the following:
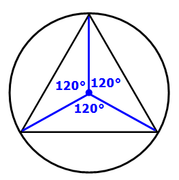
Image

Since the radii have length 4, we can add that here:
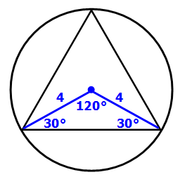
Image

Now we'll draw a line from the center that is PERPENDICULAR to one side of the tirangle.
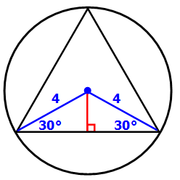
Image
We now have a SPECIAL 30-60-90 right triangle.

Here's the base version of this SPECIAL TRIANGLE
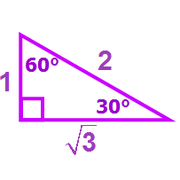
Image

We can see that the each 30-60-90 triangle in the diagram is TWICE as big as the base version. So, each side opposite the 60º angle must have length 2√3
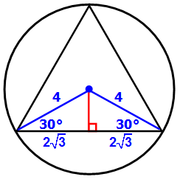
Image

This means ONE side of the equilateral triangle has length 4√3, so the PERIMETER = 4√3 + 4√3 + 4√3 = 12√3

Answer: C

Cheers,
Brent
Last edited by Brent@GMATPrepNow on Thu Apr 19, 2018 1:18 pm, edited 1 time in total.
Brent Hanneson - Creator of GMATPrepNow.com
Image
Top
Join the discussion
Log in to postLogin with Googleuse password
QUOTE IN REPLY

GMAT/MBA Expert

User avatar
Elite Legendary Member
Posts: 10392
Joined: Sun Jun 23, 2013 6:38 pmFollowed by: 511 members
Location: Palo Alto, CA
Thanked: 2867 times
GMAT Score:800

by [email protected] » Sun Oct 05, 2014 10:15 am
Hi RiyaR,

The answer choices to this question are written in such a way so that you can logically get to the correct answer and avoid most of the math. Here's why:

We're told that the radius of the circle = 4, so the diameter = 8.

An equilateral triangle inscribed into a circle will have 3 equal sides that are each GREATER than the radius but LESS than the diameter. We're asked to figure out the perimeter of the triangle.

3(radius) = 12 --> too small
3(diameter) = 24 --> too big

With this, we can eliminate A and B (too small) and E (too big)

With the remaining two answers (12root3 and 12root2), we have to think about which root we're likely to be dealing with. An equilateral triangle has three 60 degree angles in it, so we should be able to break this triangle into smaller triangles (probably a bunch of 30/60/90 triangles - which include a root3 in the "math" for figuring out some of the side lengths). It stands to reason that root3 would be part of the final calculation.

Final Answer: C

GMAT assassins aren't born, they're made,
Rich
Contact Rich at [email protected]
Image
Top
Join the discussion
Log in to postLogin with Googleuse password
QUOTE IN REPLY
Senior | Next Rank: 100 Posts
Posts: 38
Joined: Mon Sep 22, 2014 10:05 am
Thanked: 1 times

by Jacob003 » Tue Oct 07, 2014 9:50 am
Vertices of a quadrilateral ABCD are A(0, 0), B(4, 5), C(9, 9) and D(5, 4). What is the shape of the quadrilateral?
you can check for more questions here https://questionbank.4gmat.com/mba_prep_ ... s/geometry/
Top
Join the discussion
Log in to postLogin with Googleuse password
QUOTE IN REPLY
Newbie | Next Rank: 10 Posts
Posts: 1
Joined: Tue Dec 29, 2015 1:02 am

by bakhtawer » Tue Dec 29, 2015 2:37 am
Hi I can't seem to find videos for Coordinate geometry in the geometry module.Could anyone guide me >
Top
Join the discussion
Log in to postLogin with Googleuse password
QUOTE IN REPLY

GMAT/MBA Expert

User avatar
GMAT Instructor
Posts: 16207
Joined: Mon Dec 08, 2008 6:26 pmFollowed by: 1268 members
Location: Vancouver, BC
Thanked: 5254 times
GMAT Score:770

by Brent@GMATPrepNow » Tue Dec 29, 2015 5:49 am
IMO, coordinate geometry is more about solutions to equations than it is to geometry.
We (GMAT Prep Now) place it in our Algebra & Equation-Solving module (https://www.gmatprepnow.com/module/gmat- ... on-solving)

See videos #43 to #54

Cheers,
Brent
Last edited by Brent@GMATPrepNow on Tue May 17, 2016 3:54 pm, edited 1 time in total.
Brent Hanneson - Creator of GMATPrepNow.com
Image
Top
Join the discussion
Log in to postLogin with Googleuse password
QUOTE IN REPLY

GMAT/MBA Expert

User avatar
Elite Legendary Member
Posts: 10392
Joined: Sun Jun 23, 2013 6:38 pmFollowed by: 511 members
Location: Palo Alto, CA
Thanked: 2867 times
GMAT Score:800

by [email protected] » Tue Dec 29, 2015 10:09 pm
Hi bakhtawer,

You've mentioned that you can't find certain videos in the materials that you're using - but what resources are you currently using to study for the GMAT?

GMAT assassins aren't born, they're made,
Rich
Contact Rich at [email protected]
Image
Top
Join the discussion
Log in to postLogin with Googleuse password
QUOTE IN REPLY
Senior | Next Rank: 100 Posts
Posts: 64
Joined: Wed Dec 08, 2010 10:55 pm
Thanked: 1 times

by prada » Tue May 17, 2016 2:37 pm
Hey Guys, maybe there is some concepts I am missing but how did Brent conclude that the angles of the triangle are 120 degrees? From there the vertices would be radii? Is there some rule about inscribed equilateral triangles I don't know? I was trying to imagine the shape of the inscribed triangle in my head and I was thinking hmmmm maybe the base of the triangle could be the diameter of the circle maybe not? thx
Top
Join the discussion
Log in to postLogin with Googleuse password
QUOTE IN REPLY

GMAT/MBA Expert

User avatar
Elite Legendary Member
Posts: 10392
Joined: Sun Jun 23, 2013 6:38 pmFollowed by: 511 members
Location: Palo Alto, CA
Thanked: 2867 times
GMAT Score:800

by [email protected] » Tue May 17, 2016 11:03 pm
Hi prada,

There are a few specific rules at play in this question that help to make the deductions that come later:

1) The triangle is EQUILATERAL, which means that the 3 sides are the SAME length (and by extension, none of them could be the diameter of the circle - since a diameter is the longest distance between any two points on the circle, you can't make a triangle with three of those lengths).
2) Since the triangle is INSCRIBED, and each of the vertices is the same distance from the center of the circle, that triangle can be 'cut into' three identical ISOSCELES triangles.
3) Those 3 identical isosceles triangles are centered around the center of the circle. Since a circle is 360 degrees, and the triangles are identical, each of those 'central' angles is 120 degrees (and by extension, each of the triangles is a 30/30/120 triangle - and each of THOSE triangles can be cut into two 30/60/90 triangles).

GMAT assassins aren't born, they're made,
Rich
Contact Rich at [email protected]
Image
Top
Join the discussion
Log in to postLogin with Googleuse password
QUOTE IN REPLY
Senior | Next Rank: 100 Posts
Posts: 64
Joined: Wed Dec 08, 2010 10:55 pm
Thanked: 1 times

by prada » Wed May 18, 2016 7:04 am
[email protected] wrote:Hi prada,

There are a few specific rules at play in this question that help to make the deductions that come later:

1) The triangle is EQUILATERAL, which means that the 3 sides are the SAME length (and by extension, none of them could be the diameter of the circle - since a diameter is the longest distance between any two points on the circle, you can't make a triangle with three of those lengths).
2) Since the triangle is INSCRIBED, and each of the vertices is the same distance from the center of the circle, that triangle can be 'cut into' three identical ISOSCELES triangles.
3) Those 3 identical isosceles triangles are centered around the center of the circle. Since a circle is 360 degrees, and the triangles are identical, each of those 'central' angles is 120 degrees (and by extension, each of the triangles is a 30/30/120 triangle - and each of THOSE triangles can be cut into two 30/60/90 triangles).

GMAT assassins aren't born, they're made,
Rich
Cool, thanks Rich. I dont recall ever seeing that info in Magoosh or MGMAT study guides. Of course that can be deduced by knowing the "elementary" rules and properties. These are things I need to study and think about more. thx
Top
Join the discussion
Log in to postLogin with Googleuse password
QUOTE IN REPLY
Senior | Next Rank: 100 Posts
Posts: 38
Joined: Thu Apr 28, 2016 7:17 pm
Thanked: 1 times

by Gurpreet singh » Tue Jun 07, 2016 6:42 am
Formula for radius of an inscribed equilateral triangle =a/root3

ie r=a/root3

r=4
a=side of the traingle

ie
4=a/root3=4root3=a multiply both the sides by 3(perimeter of a traingle is sum of 3 sides)

ans-12root3[/spoiler][/list]
Top
Join the discussion
Log in to postLogin with Googleuse password
QUOTE IN REPLY
GMAT Instructor
Posts: 2630
Joined: Wed Sep 12, 2012 3:32 pmFollowed by: 119 members
Location: East Bay all the way
Thanked: 625 times
GMAT Score:780

by Matt@VeritasPrep » Tue Jun 07, 2016 11:07 pm
Brent@GMATPrepNow wrote:IMO, coordinate geometry is more about solutions to equations than it is to geometry.
Totally agree!

Also think that geometry seems to be dying on the GMAT: there is so much less of it these days, particularly the more elaborate questions. That can always change, but the more arcane (by GMAT standards) geometric properties seem less relevant than ever.
Top
Join the discussion
Log in to postLogin with Googleuse password
QUOTE IN REPLY
Post new topic Post Reply
• Page 1 of 1