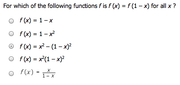For which of the following functions f is f(x)=f(1-x) for all x?

A) f(x) = 1-x
B) f(x) = 1-x²
C) f(x) = x² - (1-x)²
D) f(x) = x²(1-x)²
E) f(x) = x/(1-x)

Let's use the INPUT-OUTPUT approach.
So, let's use a "nice" value for x.
How about x = 0?

So, we can reword the question as, For which of the following functions is f(0)=f(1-0)
In other words, we're looking for a function such that f(0) = f(1)

A) f(x)=1-x
f(0)=1-0 = 1
f(1)=1-1 = 0
Since f(0) doesn't equal f(1), eliminate A

B) f(x) = 1 - x²
f(0) = 1 - 0² = 1
f(1) = 1 - 1² = 0
Since f(0) doesn't equal f(1), eliminate B

C) f(x) = x² - (1-x)²
f(0) = 0² - (1-0)² = -1
f(1) = 1² - (1-1)² = 1
Since f(0) doesn't equal f(1), eliminate C

D) f(x) = x²(1-x)²
f(0) = 0^2(1-0)^2 = 0
f(1) = 1^2(1-1)^2 = 0
Since f(0) equals f(1), keep D for now

E) f(x) = x/(1-x)
f(0) = 0/(1-0) = 0
f(1) = 1/(1-1) = undefined
Since f(0) doesn't equal f(1), eliminate E

Since only D satisfies the condition that f(x)=f(1-x) when x=0, the correct answer is D

Here's a similar question: https://www.beatthegmat.com/number-systems-t270738.html


Cheers,
Brent