Problem Solving

A cylinder is placed inside of a sphere in such a way that axis of cylinder passes through the center of the sphere. The volume of the sphere is 36pi. If the radius of the cylinder is 2/3 rd the radius of the sphere, and if the cylinder completely fills the sphere, what is the height of the cylinder ?
volume of sphere is (4/3) pi r^3

A) 2
B) root(5)
C) 2 root(2)
D) 2 root(5)
E) 6

OA D

It should be A)

Answer should 9 = height of cylinder

volume of sphere = 4/3 pi r^3 = 36 pi

r^3 = 36 * 3/4 = 27

r =3

radius of cylinder = 2/3 of 3 = 2

volume of cylinder = pi * 2^2 * h = 36 pi

4 * h = 36

h =9

@nikhilgmat31 : 36pi is the vol of sphere not cylinder.

yes kanwar, But it is also mentioned as " if the cylinder completely fills the sphere,"

A cylinder is placed inside of a sphere in such a way that axis of cylinder passes through the center of the sphere. The volume of the sphere is 36pi. If the radius of the cylinder is 2/3 rd the radius of the sphere, and if the cylinder completely fills the sphere, what is the height of the cylinder ?
volume of sphere is (4/3) pi r^3

A) 2
B) root(5)
C) 2 root(2)
D) 2 root(5)
E) 6

So how about this interpretation? The cylinder completely fills the sphere doesn't mean that they have the same volume. Rather it means that the ends of the cylinder touch the surface of the sphere.

To me that would mean that if we just look at the cross section, the cylinder in the sphere becomes like a rectangle within a circle.



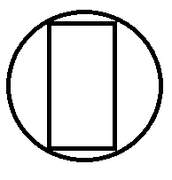
So what we need to do is find the dimensions of that rectangle, and then, because the height of the rectangle is the height of the cylinder, we will have the height of the cylinder.

First we can use the radius of the sphere to find the width of the rectangle.

If 4/3 * pi * r³ = 36pi then r of the sphere = ∛27 = 3

So if the radius of the cylinder is 2/3 the radius of the sphere, then the radius of the cylinder is 2.

That means that the top and bottom of the rectangle whose width is the diameter of the cylinder each have length 2 + 2 = 4.

Then the diagonals of the rectangle are diameters of the sphere and have length 2r = 2 * 3 = 6.

So we need the height of a rectangle that has top and bottom 4 and diagonals 6. That height is the length of the third side of a right triangle with side 4 and hypotenuse 6. So using the Pythagorean theorem, we get c² - a² = b² or 6² - 4² = 20.

So the length of the other side of the triangle is √20 = 2√5, and that is the height of the rectangle, and of the cylinder.

Choose D.

Since we know the volume of the sphere is 36Ï€, we can use the volume formula to find the radius.

36π = (4/3)πr³

27 = r³

3 = r

Now let's imagine a right triangle for which one side is the diameter of the cylinder's base, one side is the height of the cylinder, and the last side is the diagonal of the cylinder / the diameter of the sphere. Since this is a right triangle, we have

(Cylinder Base Diameter)² + (Cylinder Height)² = (Sphere Diameter)²

4² + h² = 6²

h² = 6² - 4² = 20

h = √20 = 2√5

I agree with your explanation. But in that case Question should say- cylinder fits the sphere.

well we don't have 9 as answer so I will go with your approach of solving this question.