Arrow AB, which is a line segment exactly 5 units long with an arrowhead at A, is to be constructed in the xy plane. the x and y coordinates of A and B are to be integers that satisfy inequalities
0 < or = X = or < 9
0 < or = Y = or < 9
How many different arrows with these properties can be constructed?
1) 50
2) 168
3) 200
4) 368
5) 536
536
coordinate plane question
This topic has expert replies
GMAT/MBA Expert
- Anju@Gurome
- GMAT Instructor
- Posts: 511
- Joined: Wed Aug 11, 2010 9:47 am
- Location: Delhi, India
- Thanked: 344 times
- Followed by:86 members
The arrow can be either horizontal or vertical or diagonal.
# Horizontal Arrows:
y-coordinates of A and B will be same.
For any y-coordinate, their x-coordinates can be any of the following pairs (0, 5), (5, 0), (1, 4), (4, 1), (2, 6), (6, 2), (3, 8), (8, 3), (4, 9), and (9, 4).
So, for any y-coordinate 10 horizontal arrows are possible.
There are 10 possible y-coordinates.
Hence, total number of horizontal arrows = 10*10 = 100
# Vertical Arrows:
By the same logic as above, total number of vertical arrows = 10*10 = 100
# Diagonal Arrows:
To get a diagonal arrow of length 5, we have to form a right-angled triangle whose hypotenuse is 5. Only such triangle with integral coordinates must have the lengths of other sides as 3 and 4.
Refer to the figure below,
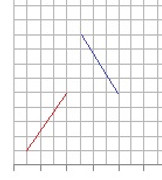
We can arrows with positive slope (red line) or arrows with negative slope (blue line)
Let us consider the arrows with positive slopes.
Note that for any particular bottom end point, we can have two diagonal line segments with positive slope of length 5 :
For case A,
Now, we can put the arrowhead in either end of the line segment.
Hence, total number of diagonal arrows with positive slope of length 5 = 2882 = 168
Similarly, there will be 168 diagonal arrows with negative slope of length 5.
Hence, total number of possible arrows of length 5 = (100 + 100 + 168 + 168) = 536
The correct answer is E.
# Horizontal Arrows:
y-coordinates of A and B will be same.
For any y-coordinate, their x-coordinates can be any of the following pairs (0, 5), (5, 0), (1, 4), (4, 1), (2, 6), (6, 2), (3, 8), (8, 3), (4, 9), and (9, 4).
So, for any y-coordinate 10 horizontal arrows are possible.
There are 10 possible y-coordinates.
Hence, total number of horizontal arrows = 10*10 = 100
# Vertical Arrows:
By the same logic as above, total number of vertical arrows = 10*10 = 100
# Diagonal Arrows:
To get a diagonal arrow of length 5, we have to form a right-angled triangle whose hypotenuse is 5. Only such triangle with integral coordinates must have the lengths of other sides as 3 and 4.
Refer to the figure below,

We can arrows with positive slope (red line) or arrows with negative slope (blue line)
Let us consider the arrows with positive slopes.
Note that for any particular bottom end point, we can have two diagonal line segments with positive slope of length 5 :
- A. base = 3, height = 4
OR
B. base = 4 and height = 3
For case A,
- The x-coordinate of the bottom end point can be any of the following : 0, 1, 2, 3, 4, 5, and 6
The y-coordinate of the bottom end point can be any of the following : 0, 1, 2, 3, 4, and 5
Possible number of diagonal line segments with positive slope of length 5 = 7*6 = 42
- The x-coordinate of the bottom end point can be any of the following : 0, 1, 2, 3, 4, and 5
The y-coordinate of the bottom end point can be any of the following : 0, 1, 2, 3, 4, 5, and 6
Possible number of diagonal line segments with positive slope of length 5 = 6*7 = 42
Now, we can put the arrowhead in either end of the line segment.
Hence, total number of diagonal arrows with positive slope of length 5 = 2882 = 168
Similarly, there will be 168 diagonal arrows with negative slope of length 5.
Hence, total number of possible arrows of length 5 = (100 + 100 + 168 + 168) = 536
The correct answer is E.
Last edited by Anju@Gurome on Fri Apr 19, 2013 6:53 am, edited 1 time in total.
Anju Agarwal
Quant Expert, Gurome
Backup Methods : General guide on plugging, estimation etc.
Wavy Curve Method : Solving complex inequalities in a matter of seconds.
§ GMAT with Gurome § Admissions with Gurome § Career Advising with Gurome §
Quant Expert, Gurome
Backup Methods : General guide on plugging, estimation etc.
Wavy Curve Method : Solving complex inequalities in a matter of seconds.
§ GMAT with Gurome § Admissions with Gurome § Career Advising with Gurome §
- hemant_rajput
- Master | Next Rank: 500 Posts
- Posts: 447
- Joined: Sun Apr 22, 2012 7:13 am
- Thanked: 46 times
- Followed by:13 members
- GMAT Score:700
you've taken the value of x and y to max 7 and max 6, but if horizontal and vertical distance are limit to be of length 3 and length 4 or vice-versa then x and y can go to max of 6 and 5 or vice-versa.Anju@Gurome wrote: For case A,For case B,
- The x-coordinate of the bottom end point can be any of the following : 0, 1, 2, 3, 4, 5, 6, and 7
The y-coordinate of the bottom end point can be any of the following : 0, 1, 2, 3, 4, 5, and 6
Possible number of diagonal line segments with positive slope of length 5 = 7*6 = 42
- The x-coordinate of the bottom end point can be any of the following : 0, 1, 2, 3, 4, 5, and 6, and 7
The y-coordinate of the bottom end point can be any of the following : 0, 1, 2, 3, 4, 5, 6, and 7
Can you please explain this?
I'm no expert, just trying to work on my skills. If I've made any mistakes please bear with me.
GMAT/MBA Expert
- Anju@Gurome
- GMAT Instructor
- Posts: 511
- Joined: Wed Aug 11, 2010 9:47 am
- Location: Delhi, India
- Thanked: 344 times
- Followed by:86 members
You're absolutely correct.hemant_rajput wrote:you've taken the value of x and y to max 7 and max 6, but if horizontal and vertical distance are limit to be of length 3 and length 4 or vice-versa then x and y can go to max of 6 and 5 or vice-versa.
Can you please explain this?
I've calculated a total of 6 and 7 possible co-ordinates but while writing down the possible values of co-ordinates, by mistake I have included '6' and '7' as the maximum values.
Edited my reply.
Anju Agarwal
Quant Expert, Gurome
Backup Methods : General guide on plugging, estimation etc.
Wavy Curve Method : Solving complex inequalities in a matter of seconds.
§ GMAT with Gurome § Admissions with Gurome § Career Advising with Gurome §
Quant Expert, Gurome
Backup Methods : General guide on plugging, estimation etc.
Wavy Curve Method : Solving complex inequalities in a matter of seconds.
§ GMAT with Gurome § Admissions with Gurome § Career Advising with Gurome §
- mariofelixpasku
- Senior | Next Rank: 100 Posts
- Posts: 41
- Joined: Sun Sep 23, 2012 4:26 am
- Thanked: 2 times
GMAT/MBA Expert
- Anju@Gurome
- GMAT Instructor
- Posts: 511
- Joined: Wed Aug 11, 2010 9:47 am
- Location: Delhi, India
- Thanked: 344 times
- Followed by:86 members
I think you meant to say 'calculations', calculus is a different thing and beyond the scope of GMAT.mariofelixpasku wrote:theres a lot of calculus to be done. can be expect sthg like that on the real gmat ?
Anyway, this problem is not at all calculation intensive. There are a number of problems in OG itself that asks for much more calculation than this one. However, this one is a bit lengthy as we need to consider different possible scenarios. GMAT generally do not ask to solve lengthy problems. However, we can expect similar problems based on the concepts of counting lines/triangles with integral coefficients on the coordinate plane. For example >> https://www.beatthegmat.com/og-12-229-60 ... tml#612443
Anju Agarwal
Quant Expert, Gurome
Backup Methods : General guide on plugging, estimation etc.
Wavy Curve Method : Solving complex inequalities in a matter of seconds.
§ GMAT with Gurome § Admissions with Gurome § Career Advising with Gurome §
Quant Expert, Gurome
Backup Methods : General guide on plugging, estimation etc.
Wavy Curve Method : Solving complex inequalities in a matter of seconds.
§ GMAT with Gurome § Admissions with Gurome § Career Advising with Gurome §


















