shivanigs wrote:Hi,
Request help with the following question.Thanks..
Point P (a,b) is randomly selected within the region enclosed by the following lines : 3y + 2x = 6, x=0 and y = 0. What is the probability that b>a ?
Hi Shivanings!
The way the problem is currently written puts this well outside of the scope of GMAT-likely questions, but it might be fun to investigate the concepts none-the-less. Now, Jim is exactly right about listing the possible Point's for P, but that assumes that a and b are integers (something your problem did not specify). So in order to figure out this probability, we will have to approach this in a slightly different way. I will need to assume that the point (a,b) can lie on the lines listed or this gets into some really ugly theoretical math that we just don't want to bother with in this forum (a graduate math class would be a better option).
So, let's start by graphing the space in question - bounded by the lines 3y+2x=6, x=0, and y=0. To make this easy, let's find the intercepts for the 3y+2x=6 line by setting each value (x and y) equal to zero and calculating the corresponding value.
3y+2(0)=6 --> 3y=6 --> y=2
so when x=0, y=2... (0,2) is a point on the line
3(0)+2x=6 --> 2x=6 --> x=3
so when y=0, x=3... (3,0) is a point on the line.
The line x=0 would be all points where the x value is 0, so this is actually the Y-axis, and the converse is true for the line y=0. So the graph would like like the following, with the region shaded in green.
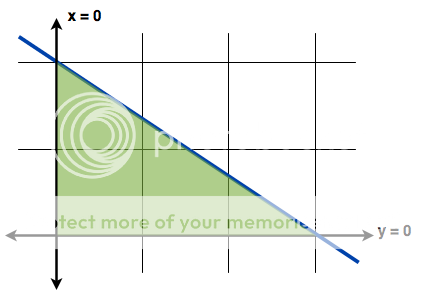
Now, we want the probability that b>a. In other words, I want all of the points in that triangle where the Y-coordinate is larger than the X-coordinate. The only way to find these would be to understand the concept of the line x=y. This is a diagonal line from the origin, with a positive slope that cuts the 3rd and 1st quadrants exactly in half (the red line in the image below). Along this line, the points share the trait that the x and y values are the same - e.g. (1,1), (0.5,0.5), (3.2,3.2), etc. To the left of (or above) this line are all the points where the y-values are greater than the x-values, and to the right is the exact opposite.
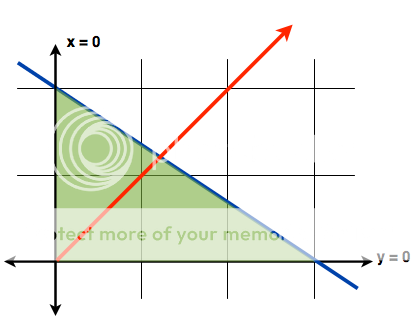
So, when we want to find the probability that our Point P (a,b) will have b>a, then we want to find the probability that the point lies to the left of the x=y line in our shaded area. Now we have to add the idea of probability as an area. What fraction of the total area of the shaded region is to the left of the red line? This means we will have to find the areas of both the large shaded region (triangle) and the smaller region to the left (also a triangle). To find the area of the whole triangle isn't too bad.
1/2(base)(height) = 1/2(3)(2) = 3.
But how do we find the area of the small triangle? We have to get creative to find our base and our height. Remember, the height has to hit one of the corners and then drop to the opposite side at a 90-degree angle. So what if we draw it with the following (the pink dashed line). The base of that small triangle would be 2 (the base is now vertically oriented), and the height would be whatever the x-coordinate is for that point.
So now comes the last big cognitive leap - how to find points of intersection. Well, to find where 2 lines intersect, we really just need to solve the system of equations for those 2 lines. We have 3y+2x=6 and x=y, so why don't we substitute in for y...
3(x) + 2x = 6
5x = 6
x = 6/5 (since this point is on the line x=y, the corresponding y would also be y=6/5, pretty nice huh!)
Okay, so the small triangle has an area 1/2(2)(6/5) = 6/5.
The probability of falling in this triangle out of the entire region is just the fraction of the total area made up of this area:
AreaSmallTriangle/AreaWholeTriangle = (6/5)/(3) = (6/5)*(1/3)
= 2/5, 0.4 or 40%.
To check your work (when practicing at home) it might be nice to find the area of the other triangle to verify that it gives you a probability of 60%. (Hint: drop a height from the same point to the x-axis this time...now we have a triangle with base 3 and height 6/5, when you calculate its area and the fraction of the total area, do you get 60%? - you should!!)
I hope this helps, but please note that a problem with this many steps and this many layers will only show up on the GMAT at the very hardest of levels, and at that point I don't care about getting it right! Remember, to get a great score the key is to knock out the easy stuff - we don't really care how we do on the hardest problems!!
Hope this helps!
Whit
