Data Sufficiency

sachindia wrote:If the area of a parallelogram is 100, what is the perimeter of the parallelogram?

1) The base of the parallelogram is 10.
2) One of the angles of the parallelogram is 45 degrees.

OA later! :mrgreen:

Target question: What is the perimeter of the parallelogram?

Given: The area is 100

Statement 1: The base of the parallelogram is 10.
Since the area of a parallelogram = (base)(height), we now know that the height of the parallelogram is 10.
Does this provide enough information to find the perimeter?
No.
It could be the case that the parallelogram is a square . . .

. . . in which case the perimeter is 40

Or it could be the case that the parallelogram is not a square . . .

. . . in which case the perimeter is not 40

Since we cannot answer the target question with certainty, statement 1 is NOT SUFFICIENT


Statement 2: One of the angles of the parallelogram is 45 degrees.
Edited to reflect Anurag's comments below
Let's let the length of the base = x
If the area of the parallelogram is 100 (and the base has length x), then the height must must be 100/x
So, at this point, we know that our parallelogram looks something like this:


Now, notice that we can extend two sides to get a convenient 45-45-90 triangle:


Since we have the lengths of 2 sides of this special right triangle, we can find the length of the 3rd side:


Since the opposite sides of a parallelogram have equal lengths, the perimeter = x + x + (sqrt2)(100/x) + (sqrt2)(100/x)

As you can see, the perimeter of the parallelogram will fluctuate, depending on the value of x.
As such, statement 2 is NOT SUFFICIENT

Statements 1 and 2 combined:
From statement 2, we know that the perimeter = x + x + (sqrt2)(100/x) + (sqrt2)(100/x)
From statement 1, we know that x = 10
So, we can plug x=10 into our formula to find the perimeter.
As such, the combined statements are SUFFICIENT

Answer = C

Cheers,
Brent

Brent@GMATPrepNow wrote:There is an infinite number of parallelograms with these angle measurements (45-45-135-135). There are super small parallelograms and super huge parallelograms .
IMPORTANT: Each time you make one of these parallelograms bigger or smaller, the area gets bigger or smaller. So, there's only one parallelogram in the universe (with angles 45, 45, 135, 135) that has an area of 100.

I'd disagree here.
There will be infinite parallelograms in the universe (with angles 45, 45, 135, 135) that has an area of 100. Without going into mathematical details, one can visualize that once we get one such parallelogram we can slightly "squeeze" it to change the length of the sides without changing the area. For example, in the following figure both parallelograms are with angles (45, 135, 45, 135) but they may have same area.


Now the mathematical proof,
Area of parallelogram is given by (base*height), where base and height are defined as follows...


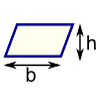
Now, b*h = 100
Assume in the first case, b = h = 10 and in the second case b = 5 and h = 20
So we have two different parallelograms with angles (45, 135, 45, 135) and area 100.

<-- Not relevant to GMAT discussion starts -->
A more methodical proof**,
Are of a parallelogram is given by ab*sin(θ), where a and b are the length of the consecutive sides and θ is the angle between them. Here, θ = 45 degrees. Hence, sin(θ) = 1/√2

Hence, ab = 100√2
Obviously the perimeter of the parallelogram = 2(a + b) can have infinite values NOT any single one.
For example,

• a = 100, b = √2 ---> 2(a + b) = 2(100 + √2)
  a = 50, b = 10√2 ---> 2(a + b) = 2(50 + 10√2)

**This is not required for GMAT. The first method is sufficient to show the insufficiency of statement 2. This is just to clarify the situation in a more generic way.
<-- Not relevant to GMAT discussion ends -->

Argh! You're absolutely right Anurag!
My bad.
I drew ONE 45-45-135-135 parallelogram and based everything else on that ONE parallelogram.
Yeesh!

I've edited my response accordingly.

Cheers,
Brent