Hello guys
I'm going to far in calculations and I get it wrong. There must be an easier way.
Here goes the question,
A small, rectangular park has a perimeter of 560 feet and a diagonal measurement of 200 feet. What is its area, in square feet?
19200 : 19600 : 20000 : 20400 : 20800.
Please let me know if you see an easier way.
Many thanks
Lukas
area
This topic has expert replies
-
lukaswelker
- Senior | Next Rank: 100 Posts
- Posts: 65
- Joined: Wed Mar 26, 2014 6:56 am
- Followed by:1 members
- theCodeToGMAT
- Legendary Member
- Posts: 1556
- Joined: Tue Aug 14, 2012 11:18 pm
- Thanked: 448 times
- Followed by:34 members
- GMAT Score:650
560 = 2 * (L + B)
L + B = 280
To find: L*B
L^2 + B^2 = (200)^2
(L+B)^2 -2*L*B = 200^2
280^2 - 200^2 = 2 * L * B
480 * 80 = 2 * L * B
L * B = 19200
L + B = 280
To find: L*B
L^2 + B^2 = (200)^2
(L+B)^2 -2*L*B = 200^2
280^2 - 200^2 = 2 * L * B
480 * 80 = 2 * L * B
L * B = 19200
R A H U L
GMAT/MBA Expert
- Brent@GMATPrepNow
- GMAT Instructor
- Posts: 16207
- Joined: Mon Dec 08, 2008 6:26 pm
- Location: Vancouver, BC
- Thanked: 5254 times
- Followed by:1268 members
- GMAT Score:770
Let L and W equal the length and width of the rectangle respectively.lukaswelker wrote: A small, rectangular park has a perimeter of 560 feet and a diagonal measurement of 200 feet. What is its area, in square feet?
A) 19200
B) 19600
C) 20000
D) 20400
E) 20800.
perimeter = 560
So, L + L + W + W = 560
Simplify: 2L + 2W = 560
Divide both sides by 2 to get: L + W = 280
diagonal = 200
The diagonal divides the rectangle into two RIGHT TRIANGLES.
Since we have right triangles, we can apply the Pythagorean Theorem.
We get L² + W² = 200²
NOTE: Our goal is to find the value of LW [since this equals the AREA of the rectangle]
If we take L + W = 280 and square both sides we get (L + W)² = 280²
If we expand this, we get: L² + 2LW + W² = 280²
Notice that we have L² + W² "hiding" in this expression.
That is, we get: L² + 2LW + W² = 280²
We already know that L² + W² = 200², so, we'll take L² + 2LW + W² = 280² and replace L² + W² with 200² to get:
2LW + 200² = 280²
So, 2LW = 280² - 200²
Evaluate: 2LW = 38,400
Solve: LW = [spoiler]19,200 = A[/spoiler]
For extra practice, here's a similar question: https://www.beatthegmat.com/area-of-a-re ... 00119.html
Cheers,
Brent
-
osama_salah
- Newbie | Next Rank: 10 Posts
- Posts: 8
- Joined: Wed Jun 15, 2016 2:05 am
How did you calculate 280² - 200² = 38,400 ?
Brent@GMATPrepNow wrote:Let L and W equal the length and width of the rectangle respectively.lukaswelker wrote: A small, rectangular park has a perimeter of 560 feet and a diagonal measurement of 200 feet. What is its area, in square feet?
A) 19200
B) 19600
C) 20000
D) 20400
E) 20800.
perimeter = 560
So, L + L + W + W = 560
Simplify: 2L + 2W = 560
Divide both sides by 2 to get: L + W = 280
diagonal = 200
The diagonal divides the rectangle into two RIGHT TRIANGLES.
Since we have right triangles, we can apply the Pythagorean Theorem.
We get L² + W² = 200²
NOTE: Our goal is to find the value of LW [since this equals the AREA of the rectangle]
If we take L + W = 280 and square both sides we get (L + W)² = 280²
If we expand this, we get: L² + 2LW + W² = 280²
Notice that we have L² + W² "hiding" in this expression.
That is, we get: L² + 2LW + W² = 280²
We already know that L² + W² = 200², so, we'll take L² + 2LW + W² = 280² and replace L² + W² with 200² to get:
2LW + 200² = 280²
So, 2LW = 280² - 200²
Evaluate: 2LW = 38,400
Solve: LW = [spoiler]19,200 = A[/spoiler]
For extra practice, here's a similar question: https://www.beatthegmat.com/area-of-a-re ... 00119.html
Cheers,
Brent
GMAT/MBA Expert
- Brent@GMATPrepNow
- GMAT Instructor
- Posts: 16207
- Joined: Mon Dec 08, 2008 6:26 pm
- Location: Vancouver, BC
- Thanked: 5254 times
- Followed by:1268 members
- GMAT Score:770
Aside: 28² = 784, which means 280² = 78,400osama_salah wrote:How did you calculate 280² - 200² = 38,400 ?
So, 280² - 200² = 78,400 - 40,000
= 38,400
- setiavipul
- Newbie | Next Rank: 10 Posts
- Posts: 1
- Joined: Tue Jun 06, 2017 9:29 am
Brent@GMATPrepNow wrote:Let L and W equal the length and width of the rectangle respectively.lukaswelker wrote: A small, rectangular park has a perimeter of 560 feet and a diagonal measurement of 200 feet. What is its area, in square feet?
A) 19200
B) 19600
C) 20000
D) 20400
E) 20800.
perimeter = 560
So, L + L + W + W = 560
Simplify: 2L + 2W = 560
Divide both sides by 2 to get: L + W = 280
diagonal = 200
The diagonal divides the rectangle into two RIGHT TRIANGLES.
Since we have right triangles, we can apply the Pythagorean Theorem.
We get L² + W² = 200²
NOTE: Our goal is to find the value of LW [since this equals the AREA of the rectangle]
If we take L + W = 280 and square both sides we get (L + W)² = 280²
If we expand this, we get: L² + 2LW + W² = 280²
Notice that we have L² + W² "hiding" in this expression.
That is, we get: L² + 2LW + W² = 280²
We already know that L² + W² = 200², so, we'll take L² + 2LW + W² = 280² and replace L² + W² with 200² to get:
2LW + 200² = 280²
So, 2LW = 280² - 200²
Evaluate: 2LW = 38,400
Solve: LW = [spoiler]19,200 = A[/spoiler]
For extra practice, here's a similar question: https://www.beatthegmat.com/area-of-a-re ... 00119.html
Cheers,
Brent
Why we can not use 45,45,90 degree property here? Diagonal of a rectangle divides two sides into 45 and 45 degree angle. Am i wrong here?
- GMATGuruNY
- GMAT Instructor
- Posts: 15539
- Joined: Tue May 25, 2010 12:04 pm
- Location: New York, NY
- Thanked: 13060 times
- Followed by:1906 members
- GMAT Score:790
ALWAYS LOOK FOR SPECIAL TRIANGLES.A small rectangular park has a perimeter of 560 feet and a diagonal measurement of 200 feet. What is its area, in square feet?
a/ 19200
b/ 19600
c/ 20000
d/ 20400
e/ 20800
Draw the rectangle and its diagonal:
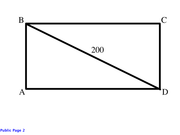
Since diagonal AD is a multiple of 5, check whether ∆ABD is a multiple of a 3:4:5 triangle.
If each side of a 3:4:5 triangle is multiplied by 40, we get::
(40*3):(40*4):(40*5) = 120:160:200.
The following figure is implied:
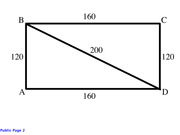
Check whether the resulting perimeter for rectangle ABCD is 560:
120+160+120+160 = 560.
Success!
Implication:
For the perimeter of rectangle ABCD to be 560, ∆ABD must be a multiple of a 3:4:5 triangle with sides 120, 160 and 200.
Thus:
Area of rectangle ABCD = L * W = 160 * 120 = 19200.
The correct answer is A.
Private tutor exclusively for the GMAT and GRE, with over 20 years of experience.
Followed here and elsewhere by over 1900 test-takers.
I have worked with students based in the US, Australia, Taiwan, China, Tajikistan, Kuwait, Saudi Arabia -- a long list of countries.
My students have been admitted to HBS, CBS, Tuck, Yale, Stern, Fuqua -- a long list of top programs.
As a tutor, I don't simply teach you how I would approach problems.
I unlock the best way for YOU to solve problems.
For more information, please email me (Mitch Hunt) at [email protected].
Student Review #1
Student Review #2
Student Review #3
Followed here and elsewhere by over 1900 test-takers.
I have worked with students based in the US, Australia, Taiwan, China, Tajikistan, Kuwait, Saudi Arabia -- a long list of countries.
My students have been admitted to HBS, CBS, Tuck, Yale, Stern, Fuqua -- a long list of top programs.
As a tutor, I don't simply teach you how I would approach problems.
I unlock the best way for YOU to solve problems.
For more information, please email me (Mitch Hunt) at [email protected].
Student Review #1
Student Review #2
Student Review #3
GMAT/MBA Expert
- [email protected]
- Elite Legendary Member
- Posts: 10392
- Joined: Sun Jun 23, 2013 6:38 pm
- Location: Palo Alto, CA
- Thanked: 2867 times
- Followed by:511 members
- GMAT Score:800
Hi All,
It's important to remember that nothing about a GMAT question is ever 'random' - the wording and numbers/data are always carefully chosen. Thus, you can sometimes use the 'design' of a prompt to your advantage and spot the built-in patterns that are often there.
Here, notice how ALL of the numbers are relatively 'nice', round numbers - even the diagonal is a nice number (and that doesn't happen very often when dealing with rectangles).... Since the answer choices are also round numbers, it's likely that the triangles that are 'hidden' in this rectangle are based on one of the common right-triangle patterns (in this case, the 3/4/5 - since 200 is a multiple of 5).
Using that knowledge to our advantage, IF we had a 3/4/5 and the diagonal was 200, then that would be '40 times' 5... so the other two sides would be 40 times 4 and 40 times 3: 160 and 120. With those two side lengths, we'd have a perimeter of 2(160) + 2(120) = 560... and that is an exact MATCH for what we were told, so this MUST be the situation that we're dealing with.
At this point, the area can be calculated easily enough: (L)(W) = (160)(120) = 19,200
Final Answer: A
GMAT assassins aren't born, they're made,
Rich
It's important to remember that nothing about a GMAT question is ever 'random' - the wording and numbers/data are always carefully chosen. Thus, you can sometimes use the 'design' of a prompt to your advantage and spot the built-in patterns that are often there.
Here, notice how ALL of the numbers are relatively 'nice', round numbers - even the diagonal is a nice number (and that doesn't happen very often when dealing with rectangles).... Since the answer choices are also round numbers, it's likely that the triangles that are 'hidden' in this rectangle are based on one of the common right-triangle patterns (in this case, the 3/4/5 - since 200 is a multiple of 5).
Using that knowledge to our advantage, IF we had a 3/4/5 and the diagonal was 200, then that would be '40 times' 5... so the other two sides would be 40 times 4 and 40 times 3: 160 and 120. With those two side lengths, we'd have a perimeter of 2(160) + 2(120) = 560... and that is an exact MATCH for what we were told, so this MUST be the situation that we're dealing with.
At this point, the area can be calculated easily enough: (L)(W) = (160)(120) = 19,200
Final Answer: A
GMAT assassins aren't born, they're made,
Rich
GMAT/MBA Expert
- Brent@GMATPrepNow
- GMAT Instructor
- Posts: 16207
- Joined: Mon Dec 08, 2008 6:26 pm
- Location: Vancouver, BC
- Thanked: 5254 times
- Followed by:1268 members
- GMAT Score:770
That rule doesn't apply to rectangles. It does, however apply to squaressetiavipul wrote: Why we can not use 45,45,90 degree property here? Diagonal of a rectangle divides two sides into 45 and 45 degree angle. Am i wrong here?
Cheers,
Brent
- DavidG@VeritasPrep
- Legendary Member
- Posts: 2663
- Joined: Wed Jan 14, 2015 8:25 am
- Location: Boston, MA
- Thanked: 1153 times
- Followed by:128 members
- GMAT Score:770
Note also, that if the figure were a square, and the perimeter were 560, each side would be 560/4 = 140. If each side of a 45/45/90 triangle were 140, the hypotenuse, or diagonal, would be 140 *rt2. So the fact that the diagonal is 200 tells us that we're not dealing with a square (or 45:45:90 triangles.)Why we can not use 45,45,90 degree property here? Diagonal of a rectangle divides two sides into 45 and 45 degree angle. Am i wrong here?
- DavidG@VeritasPrep
- Legendary Member
- Posts: 2663
- Joined: Wed Jan 14, 2015 8:25 am
- Location: Boston, MA
- Thanked: 1153 times
- Followed by:128 members
- GMAT Score:770
One more fun note. For a set perimeter, the rectangle with the greatest area is a square. If the shape in question had been a square, and the sides had each been 140, the area would have been 140*140 = 19,600. Because we know the shape is not a square, we know the area would be less than 19,600. The answer must be ADavidG@VeritasPrep wrote:Note also, that if the figure were a square, and the perimeter were 560, each side would be 560/4 = 140. If each side of a 45/45/90 triangle were 140, the hypotenuse, or diagonal, would be 140 *rt2. So the fact that the diagonal is 200 tells us that we're not dealing with a square (or 45:45:90 triangles.)Why we can not use 45,45,90 degree property here? Diagonal of a rectangle divides two sides into 45 and 45 degree angle. Am i wrong here?
-
Matt@VeritasPrep
- GMAT Instructor
- Posts: 2630
- Joined: Wed Sep 12, 2012 3:32 pm
- Location: East Bay all the way
- Thanked: 625 times
- Followed by:119 members
- GMAT Score:780
I love that, nice hack!DavidG@VeritasPrep wrote:One more fun note. For a set perimeter, the rectangle with the greatest area is a square. If the shape in question had been a square, and the sides had each been 140, the area would have been 140*140 = 19,600. Because we know the shape is not a square, we know the area would be less than 19,600. The answer must be ADavidG@VeritasPrep wrote:Note also, that if the figure were a square, and the perimeter were 560, each side would be 560/4 = 140. If each side of a 45/45/90 triangle were 140, the hypotenuse, or diagonal, would be 140 *rt2. So the fact that the diagonal is 200 tells us that we're not dealing with a square (or 45:45:90 triangles.)Why we can not use 45,45,90 degree property here? Diagonal of a rectangle divides two sides into 45 and 45 degree angle. Am i wrong here?





















