Problem Solving

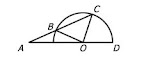
In the figure shown, point O is the center of the semicircle and points B, C, and D lie on the semicircle. If the length of line segment AB is equal to the length of line sement OC, what is the degree measure of angle BAO?

(1) The degree measure of angle COD is 60º
(2) The degree measure of angle BCO is 40º

Target question: What is the degree measure of ∠BAO?

Given: The length of line segment AB is equal to the length of line sement OC

Statement 1: The degree measure of angle COD is 60º
So, we have the following:


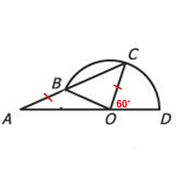
Since the radii must have equal lengths, we can see that OB = OC


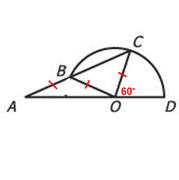
So, ∆ABO is an isosceles triangle.


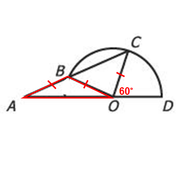
If we let ∠BAO = x degrees, then we can use the facts that ∆ABO is isosceles and that angles must add to 180º to get the following:


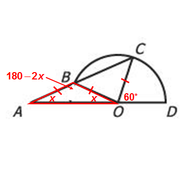
Since angles on a LINE must add to 180º, we know that ∠OBC = 2x


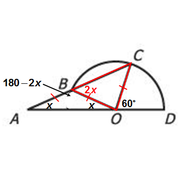
Now, we can use the facts that ∆BCO is isosceles and that the angles must add to 180º to get the following:


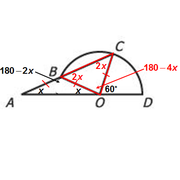
Finally, we can see that the 3 angles with blue circles around them are on a line.

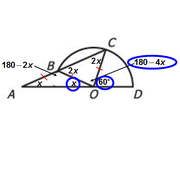
So, they must add to 180 degrees.
We get: x + (180-4x) + 60 = 180
Simplify: 240 - 3x = 180
Solve to get: x = 20
In other words, ∠BAO = 20º
Since we can answer the target question with certainty, statement 1 is SUFFICIENT

Statement 2: The degree measure of angle BCO is 40º
So, we have the following:


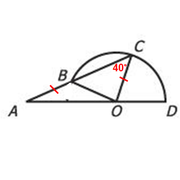
Since the radii must have equal lengths, we can see that OB = OC


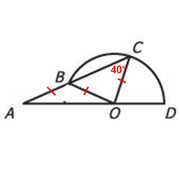
So, ∆BCO is an isosceles triangle, which means OBC is also 40º


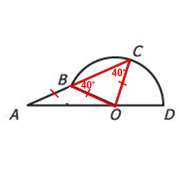
Since angles on a line must add to 180 degrees, ∠ABO = 140º


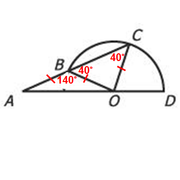
Finally, since ∆ABO is an isosceles triangle, the other two angles must each be 20º

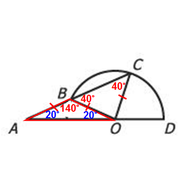
As we can see, ∠BAO = 20º
Since we can answer the target question with certainty, statement 2 is SUFFICIENT

Answer = D

Cheers,
Brent