Problem Solving

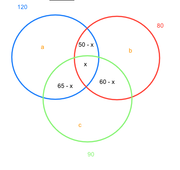
How to do the below question both in venn diagram approach and formulae approach and which approach is best under time constraints ?

In a hostel there are 250 students, 120 watch Fox News, 80 watch Sky Sports, and 90 watch ABC. 50 students watch both Fox News and Sky Sports, 60 students watch both Sky sports and ABC and 65 students watch both Fox News and ABC. What is the minimum number of students who watch atleast one of the given channels?
A.35
B.50
C.135
D.150
E.165

OA is D

Thanks
Vinni

vinni.k wrote:How to do the below question both in venn diagram approach and formulae approach and which approach is best under time constraints ?

In a hostel there are 250 students, 120 watch Fox News, 80 watch Sky Sports, and 90 watch ABC. 50 students watch both Fox News and Sky Sports, 60 students watch both Sky sports and ABC and 65 students watch both Fox News and ABC. What is the minimum number of students who watch at least one of the given channels?
A.3550
B.50
C.135
D.150
E.165

One formula for 3 overlapping sets is as follows:

Total = Group 1 + Group 2 + Group 3 - (at least 2 of the groups) + (all 3 groups) + none.

In the problem above:
Total = 250.
Group 1 = 120.
Group 2 = 80.
Group 3 = 90.
(at least 2 of the groups) = 50+60+65 = 175.
Let x = all 3.
Let N = none.

Plugging these values into the equation above, we get:
250 = 120 + 80 + 90 - 175 + x + N.
250 = 115 + x + N
N = 250 - 115 - x.
N = 135 - x.

To MINIMIZE the number who watch at least 1 channel, we must MAXIMIZE the value of N: the number who watch NONE of the channels.
In the blue equation above, the value of N will be maximized if x is as small as possible.

Of the given overlaps -- 50, 60, 65 -- the two greatest overlaps both include A:
(at least S and A) + (at least F and A) = 60+65 = 125.
The value in red is 35 greater than the total number who watch A (90).
Implication:
At least 35 students must watch all 3 channels.
Thus, the minimum value of x = 35.

Plugging x=35 into N = 135 - x, we get:
N = 135 - 35 = 100.
Since the maximum number who watch none of the channels = 100, the minimum number who watch at least 1 channel = 250-100 = 150.

The correct answer is D.

How can I solve this using tables?

Mitch,

thanks for the explanation. Nice explanation and very well understood.

I just have one small question - when can we take none as 0 ?

The question asks "What is the minimum number of students who watch at least one of the given channels ?"

Here students must be watching 1 channel if not 2 or 3. So, why none can't be 0 ?

Please check the similar question in which none is taken as "0"
https://gmatclub.com/forum/workers-are-g ... 90246.html

Also your link in which you have answered the above question in venn diagram approach
https://www.beatthegmat.com/overlapping- ... 86959.html

Looking forward to your reply

Thanks
Vinni

vinni.k wrote:Mitch,

thanks for the explanation. Nice explanation and very well understood.

I just have one small question - when can we take none as 0 ?

The question asks "What is the minimum number of students who watch at least one of the given channels ?"

Here students must be watching 1 channel if not 2 or 3. So, why none can't be 0 ?

If none = 0, then all 250 students watch at least one channel.
Since 250 is not among the answer choices, the number of students who watch none of the channels must be greater than 0.

Please check the similar question in which none is taken as "0"
https://gmatclub.com/forum/workers-are-g ... 90246.html

Also your link in which you have answered the above question in venn diagram approach
https://www.beatthegmat.com/overlapping- ... 86959.html

Looking forward to your reply

Thanks
Vinni

In this problem, it is stated that workers...are placed on at least one team.
Thus, the number of workers placed on none of the teams = 0.

Thanks a lot Mitch.

I have a question as to why Group A was chosen as factor for deciding min x.

In your solution you state that it is because it has the greatest overlapping sets (60+65=125). But is it not in fact because (125-90 = 35) is the greatest among all 3 possibilities?

For example, If Sky had only 60 viewers (instead of the stated 80), then x would have to be at least (50+60-60 = 50). But since Sky DOES have 80, the number is (50+60-80 = 30) which is less that 35. And this is why we choose A to compute min x, is it not?

Please do let me know if my understanding is correct.

p2tom wrote:Thanks a lot Mitch.

I have a question as to why Group A was chosen as factor for deciding min x.

In your solution you state that it is because it has the greatest overlapping sets (60+65=125). But is it not in fact because (125-90 = 35) is the greatest among all 3 possibilities?

For example, If Sky had only 60 viewers (instead of the stated 80), then x would have to be at least (50+60-60 = 50). But since Sky DOES have 80, the number is (50+60-80 = 30) which is less that 35. And this is why we choose A to compute min x, is it not?

Please do let me know if my understanding is correct.

To determine the least number who must be in all 3 groups, test every possible combination of pairings:
(at least F and S) and (at least F and A)
(at least F and S) and (at least S and A)
(at least S and A) and (at least F and A).

(at least F and S) and (at least F and A):
(at least F and S) + (at least F and A) = 50+65 = 115.
The value in red is less than the total number in F (120).
Implication:
Here, there is no need for any member to be in all 3 groups.

(at least F and S) and (at least S and A):
(at least F and S) + (at least S and A) = 50+60 = 110.
The value in red is 30 more than the total number in S (80).
Implication:
Here, at least 30 members must be in all 3 groups.

(at least S and A) and (at least F and A):
(at least S and A) + (at least F and A) = 60+65 = 125.
The value in red is 35 more than the total number in A (90).
Implication:
Here, at least 35 members must be in all 3 groups.

Thus, the smallest possible value for x = 35.

Hi Mitch,

Can this question be solved without using the formula? I am not that great with formulae and would like to know an alternative method for solving this type of question?

GMATGuruNY wrote:

vinni.k wrote:How to do the below question both in venn diagram approach and formulae approach and which approach is best under time constraints ?

In a hostel there are 250 students, 120 watch Fox News, 80 watch Sky Sports, and 90 watch ABC. 50 students watch both Fox News and Sky Sports, 60 students watch both Sky sports and ABC and 65 students watch both Fox News and ABC. What is the minimum number of students who watch at least one of the given channels?
A.3550
B.50
C.135
D.150
E.165

One formula for 3 overlapping sets is as follows:

Total = Group 1 + Group 2 + Group 3 - (at least 2 of the groups) + (all 3 groups) + none.

In the problem above:
Total = 250.
Group 1 = 120.
Group 2 = 80.
Group 3 = 90.
(at least 2 of the groups) = 50+60+65 = 175.
Let x = all 3.
Let N = none.

Plugging these values into the equation above, we get:
250 = 120 + 80 + 90 - 175 + x + N.
250 = 115 + x + N
N = 250 - 115 - x.

To MINIMIZE the number who watch at least 1 channel, we must MAXIMIZE the value of N: the number who watch NONE of the channels.
In the blue equation above, the value of N will be maximized if x is as small as possible.

Of the given overlaps -- 50, 60, 65 -- the two greatest overlaps both include A:
(at least S and A) + (at least F and A) = 60+65 = 125.
The value in red is 35 greater than the total number who watch A (90).
Implication:
At least 35 students must watch all 3 channels.
Thus, the minimum value of x = 35.

Plugging x=35 into N = 250 - 115 - x, we get:
N = 250 - 115 - 35 = 100.
Since the maximum number who watch none of the channels = 100, the minimum number who watch at least 1 channel = 250-100 = 150.

The correct answer is D.

Yup, you can do it visually! This will help you write the formulas yourself, and see what's happening:

anishab wrote:Hi Mitch,

Can this question be solved without using the formula? I am not that great with formulae and would like to know an alternative method for solving this type of question?

Hi Matt,
Thank you for the screenshot!. However, I am still confused on how it needs to be solved? and how is x=35. Maybe I am confused with the question itself. Isn't it asking the addition of all the values to get the number of students who watches "atleast one channel"? So except students who watch none we need all the values.

Matt@VeritasPrep wrote:Yup, you can do it visually! This will help you write the formulas yourself, and see what's happening: ?

anishab wrote:Hi Mitch,

Can this question be solved without using the formula? I am not that great with formulae and would like to know an alternative method for solving this type of question?