A circle is circumscribed around a square such that all the angles of the squares lie on circumference. What is the area of the circle, if area of the square is 100 units?
A. 131
B. 137
C. 157
D. 161
E. 174
I'm confused how to set up the formulas here. Can any experts help?
A circle is circumscribed around a square such that all the
This topic has expert replies
-
BTGmoderatorAT
- Moderator
- Posts: 426
- Joined: Tue Aug 22, 2017 8:48 pm
- Followed by:1 members
Given the are of the square is 100 units. So, the length of one side is 10 units.ardz24 wrote:A circle is circumscribed around a square such that all the angles of the squares lie on circumference. What is the area of the circle, if area of the square is 100 units?
A. 131
B. 137
C. 157
D. 161
E. 174
I'm confused how to set up the formulas here. Can any experts help?
The length of diagonal = sqrt(10^2+10^2) = sqrt(200)
As the circle is circumscribed around the square, its diameter is = sqrt(200) and radius = sqrt(200)/2.
Area of circle = Pi * r^2 where r is radius
= 3.1415926 * {sqrt(200)/2}^2 = 3.1415926 * 200 / 4 = 157.07963
Approximate area of circle = 157 square units. Thus, answer is C.
GMAT/MBA Expert
- Brent@GMATPrepNow
- GMAT Instructor
- Posts: 16207
- Joined: Mon Dec 08, 2008 6:26 pm
- Location: Vancouver, BC
- Thanked: 5254 times
- Followed by:1268 members
- GMAT Score:770
The question should read "What is the APPROXIMATE area?"
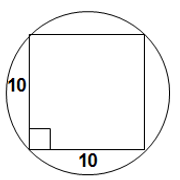
Since each vertex is a RIGHT ANGLE, we know that the diagonal (shown below) must pass through the center of the circle. In other words, the square's diagonal is also the DIAMETER of the circle.
Also, since the area of square is 100, we know that each side has length 10
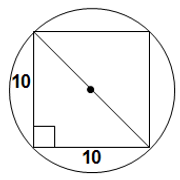
Let's let d = the length of the diameter
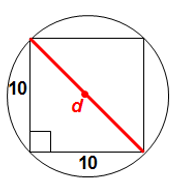
Since d also represents the HYPOTENUSE of a right triangle with the two legs each having length 10, we can apply the Pythagorean Theorem.
When we do this, we get: 10² + 10² = d²
Simplify: 200 = d²
So, d = √200
Or: d = 10√2
Add that below:
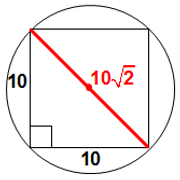
Since the circle's DIAMETER has length 10√2, we can conclude that the circle's RADIUS has length 5√2
What is the APPROXIMATE area of the circle?
Area = (pi)(radius)²
= (pi)(5√2)²
= (pi)(50)
ASIDE: What value of pi is needed here? We COULD use a very precise value of pi, like 3.1416, but that probably isn't necessary.
If we let pi = 3, then the area ≈ (3)(50) ≈ 150. However, given how close the answer choices are, I might want to be a little more precise than this.
If we let pi = 3.1, then the area ≈ (3.1)(50) ≈ 155.
This is very close to answer choice C, so C must be correct.
Cheers,
Brent
Here's a diagram of the question:ardz24 wrote:A circle is circumscribed around a square such that all the angles of the squares lie on circumference. What is the APPROXIMATE area of the circle, if area of the square is 100 units?
A. 131
B. 137
C. 157
D. 161
E. 174

Since each vertex is a RIGHT ANGLE, we know that the diagonal (shown below) must pass through the center of the circle. In other words, the square's diagonal is also the DIAMETER of the circle.
Also, since the area of square is 100, we know that each side has length 10

Let's let d = the length of the diameter

Since d also represents the HYPOTENUSE of a right triangle with the two legs each having length 10, we can apply the Pythagorean Theorem.
When we do this, we get: 10² + 10² = d²
Simplify: 200 = d²
So, d = √200
Or: d = 10√2
Add that below:

Since the circle's DIAMETER has length 10√2, we can conclude that the circle's RADIUS has length 5√2
What is the APPROXIMATE area of the circle?
Area = (pi)(radius)²
= (pi)(5√2)²
= (pi)(50)
ASIDE: What value of pi is needed here? We COULD use a very precise value of pi, like 3.1416, but that probably isn't necessary.
If we let pi = 3, then the area ≈ (3)(50) ≈ 150. However, given how close the answer choices are, I might want to be a little more precise than this.
If we let pi = 3.1, then the area ≈ (3.1)(50) ≈ 155.
This is very close to answer choice C, so C must be correct.
Cheers,
Brent
GMAT/MBA Expert
- Jeff@TargetTestPrep
- GMAT Instructor
- Posts: 1462
- Joined: Thu Apr 09, 2015 9:34 am
- Location: New York, NY
- Thanked: 39 times
- Followed by:22 members
Since the area of the square is 100 units, each side is 10.ardz24 wrote:A circle is circumscribed around a square such that all the angles of the squares lie on circumference. What is the area of the circle, if area of the square is 100 units?
A. 131
B. 137
C. 157
D. 161
E. 174
Note that the diagonal of the square = the diameter of the circle. The diagonal of the square cuts the square into two 45-45-90 triangles, and the ratio of the sides of a 45-45-90 triangle is x : x : x√2. Thus, the diagonal of the square = the diameter of the circle = 10√2, and thus the radius is 5√2.
Therefore, the area of the circle is π(5√2)^2 = 50π ≈ 50 x 3.14 = 157.
Answer: C
Jeffrey Miller
Head of GMAT Instruction
[email protected]

See why Target Test Prep is rated 5 out of 5 stars on BEAT the GMAT. Read our reviews
- EconomistGMATTutor
- GMAT Instructor
- Posts: 555
- Joined: Wed Oct 04, 2017 4:18 pm
- Thanked: 180 times
- Followed by:12 members
Hi ardz24,ardz24 wrote:A circle is circumscribed around a square such that all the angles of the squares lie on circumference. What is the area of the circle, if area of the square is 100 units?
A. 131
B. 137
C. 157
D. 161
E. 174
I'm confused how to set up the formulas here. Can any experts help?
Let's take a look at your question.
A circle is circumscribed around a square such that all the angles of the squares lie on the circumference.
The area of the square is 100 square units then each of the sides of the square will be 10 units.
It will look like this:
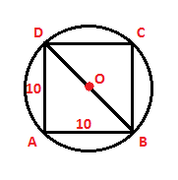
To find the area of the circle we need to find the radius of the circle, which is half the diagonal of the square.
So let's first find the diagonal of the square using Pythagoras theorem.
(Diagonal)^2 = (10)^2 + (10)^2
(Diagonal)^2 = 100 + 100
(Diagonal)^2 = 200
Diagonal = 10√2 units
Now, we can find the radius of the circle,
Radius = Diagonal / 2
r = 10√2/2
r = 5√2 units
Area of the circle can now be calculated as:
Area of circle = pi * r^2
Area of circle = 3.14 * (5√2)^2
Area of circle = 3.14 * 25 * 2
Area of circle = 157 units
Therefore, Option C is correct.
I am available if you'd like any followup.
GMAT Prep From The Economist
We offer 70+ point score improvement money back guarantee.
Our average student improves 98 points.

We offer 70+ point score improvement money back guarantee.
Our average student improves 98 points.

- EconomistGMATTutor
- GMAT Instructor
- Posts: 555
- Joined: Wed Oct 04, 2017 4:18 pm
- Thanked: 180 times
- Followed by:12 members
Hi ardz24,ardz24 wrote:A circle is circumscribed around a square such that all the angles of the squares lie on circumference. What is the area of the circle, if area of the square is 100 units?
A. 131
B. 137
C. 157
D. 161
E. 174
I'm confused how to set up the formulas here. Can any experts help?
Let's take a look at your question.
A circle is circumscribed around a square such that all the angles of the squares lie on the circumference.
The area of the square is 100 square units then each of the sides of the square will be 10 units.
It will look like this:

To find the area of the circle we need to find the radius of the circle, which is half the diagonal of the square.
So let's first find the diagonal of the square using Pythagoras theorem.
(Diagonal)^2 = (10)^2 + (10)^2
(Diagonal)^2 = 100 + 100
(Diagonal)^2 = 200
Diagonal = 10√2 units
Now, we can find the radius of the circle,
Radius = Diagonal / 2
r = 10√2/2
r = 5√2 units
Area of the circle can now be calculated as:
Area of circle = pi * r^2
Area of circle = 3.14 * (5√2)^2
Area of circle = 3.14 * 25 * 2
Area of circle = 157 units
Therefore, Option C is correct.
I am available if you'd like any followup.
GMAT Prep From The Economist
We offer 70+ point score improvement money back guarantee.
Our average student improves 98 points.

We offer 70+ point score improvement money back guarantee.
Our average student improves 98 points.





















