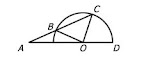
In the figure shown, point O is the center of the semicircle and points B, C, and D lie on the semicircle. If the length of line segment AB is equal to the length of line sement OC, what is the degree measure of angle BAO?
(1) The degree measure of angle COD is 60°.
(2) The degree measure of angle BCO is 40°.
I certainly dont see a way to solve this... Anybody?




















