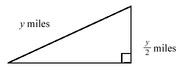
A flat triangular cornfield has the dimensions shown in the figure above. If y^2=2, what is the area of the field in square miles?

$$A.\ \frac{1}{4}$$
$$B.\ \frac{\sqrt{3}}{4}$$
$$C.\ \frac{1}{2}$$
$$D.\ \frac{\sqrt{3}}{2}$$
$$E.\ 1$$

The OA is B.

$$If\ \ y^2=2,\ \ then\ \ y=\sqrt{2}$$
The base of triangular cornfield can be determined from,
$$\sqrt{2}^2=\left(\frac{\sqrt{2}}{2}\right)^2+b^2,\ then\ b=\sqrt{\frac{3}{2}}$$
Now, we can determine the area of the field of the following way,
$$A_{\triangle}=\frac{1}{2}b\cdot h=\frac{1}{2}\sqrt{\frac{3}{2}}\cdot\frac{\sqrt{2}}{2}=\frac{1}{2}\cdot\frac{\sqrt{3}}{\sqrt{2}}\cdot\frac{\sqrt{2}}{2}=\frac{\sqrt{3}}{4}$$
Experts, any suggestion about this PS question? Thanks in advance.