There are 27 students on the collage debate team. What is the probability that at least 3 of them have their birthdays in the same month?
A. 0
B. 3/27
C. 3/12
D. 1/2
E. 1
OA: E
Solve 700-Level Algebra Qs In 90 Secs!
Master 700-level Inequalities and Absolute Value Questions
Attend this free GMAT Algebra Webinar and learn how to master the most challenging Inequalities and Absolute Value problems with ease.
Probability question
This topic has expert replies
-
[email protected]
- Legendary Member
- Posts: 2663
- Joined: Wed Jan 14, 2015 8:25 am
- Location: Boston, MA
- Thanked: 1153 times
- Followed by:128 members
- GMAT Score:770
P(at least 3 born in same month) = 1 - P(less than 3 born in same month)Mo2men wrote:There are 27 students on the collage debate team. What is the probability that at least 3 of them have their birthdays in the same month?
A. 0
B. 3/27
C. 3/12
D. 1/2
E. 1
OA: E
Notice that we can't have all 27 born in different months, as there are only 12 months. We also can't have exactly 2 born in the same month. Even if exactly 2 were born in in the first 11 months of the year, that leaves us with 5 people who must have been born in December. Thus P(less than 3 born in same month = 0)
1 - P(less than 3 born in same month) = 1 - 0 = 1. The answer is E
(So long as there are more than 24 people, this would have to be the case.)
GMAT/MBA Expert
-
[email protected]
- GMAT Instructor
- Posts: 16201
- Joined: Mon Dec 08, 2008 6:26 pm
- Location: Vancouver, BC
- Thanked: 5254 times
- Followed by:1268 members
- GMAT Score:770
This question tests a concept known as the pigeon hole principle (https://en.wikipedia.org/wiki/Pigeonhole_principle)Mo2men wrote:There are 27 students on the collage debate team. What is the probability that at least 3 of them have their birthdays in the same month?
A. 0
B. 3/27
C. 3/12
D. 1/2
E. 1
OA: E
Here's an analogous question:
If 3 candies are distributed among 2 people, what is the probability that at least person receives at least 2 candies?
Notice that, if we try to ensure that neither person receives more than 1 candy, we start by giving each person 1 candy. At that point, we still have 1 candy left to give to someone. Regardless of who we give that last remaining candy to, we will will GUARANTEE that someone receives at least 2 candies.
Cheers,
Brent
Brent Hanneson - Creator of GMATPrepNow.com
GMAT/MBA Expert
-
[email protected]
- GMAT Instructor
- Posts: 3008
- Joined: Mon Aug 22, 2016 6:19 am
- Location: Grand Central / New York
- Thanked: 470 times
- Followed by:34 members
Hi Mo2men,Mo2men wrote:There are 27 students on the collage debate team. What is the probability that at least 3 of them have their birthdays in the same month?
A. 0
B. 3/27
C. 3/12
D. 1/2
E. 1
OA: E
This is a question based on a sure event.
We have to distribute 27 birthdays among 12 months. Let's take extreme cases.
1. Assume that all 27 birthdays fall in ONLY one among 12 months. So, there is a month in which at least 3 birthdays fall in the same month. Probability = 1
2a. Let's distribute 27 birthdays equally among 12 months, and see whether there is a month(s) that have at least 3 birthdays.
Since 12*2 = 24, we must have a month that must accommodate 3 more birthdays (27 - 24 = 3), so that very month has 5 birthdays (Al least 3 birthdays). Probability = 1
2b. Another way of distribution of the remaining 3 birthdays in the case discussed above (case 2), we may have three months that each have 3 birthdays. Again the condition of at least 3 birthdays is fulfilled. Probability = 1
The correct answer: E
Hope this helps!
Relevant book: Manhattan Review GMAT Combinatorics and Probability Guide
-Jay
_________________
Manhattan Review GMAT Prep
Locations: New York | Barcelona | Manila | Melbourne | and many more...
Schedule your free consultation with an experienced GMAT Prep Advisor! Click here.
GMAT/MBA Expert
-
[email protected]
- Elite Legendary Member
- Posts: 10392
- Joined: Sun Jun 23, 2013 6:38 pm
- Location: Palo Alto, CA
- Thanked: 2867 times
- Followed by:511 members
- GMAT Score:800
Hi Kaustubhk,
This prompt is more a 'logic' problem than a math question. We have 27 students and 12 potential months in which those 27 students could possibly have their birthdays. It's possible that all 27 birthdays are in the same month or that the birthdays are "spread out" over the 12 months. We're asked for the probability that at least 3 of the birthdays are in the SAME month. Note that the prompt doesn't specify which month - so ANY month will do.
It might help to think in terms of how you might avoid having at least 3 birthdays in the same month. To do that, you would have no more than 2 birthdays per month. Over the course of 12 months, you could place (12)(2) = 24 of the birthdays and not have 3 or more in any given month. However, we have to place 27 birthdays - and if each of the 12 months already has 2 birthdays, then wherever you put those remaining 3 birthdays... there WILL be at least one month that includes at least 3 birthdays. Thus the probability of this outcome is 100% = 1.
Final Answer: E
GMAT assassins aren't born, they're made,
Rich
This prompt is more a 'logic' problem than a math question. We have 27 students and 12 potential months in which those 27 students could possibly have their birthdays. It's possible that all 27 birthdays are in the same month or that the birthdays are "spread out" over the 12 months. We're asked for the probability that at least 3 of the birthdays are in the SAME month. Note that the prompt doesn't specify which month - so ANY month will do.
It might help to think in terms of how you might avoid having at least 3 birthdays in the same month. To do that, you would have no more than 2 birthdays per month. Over the course of 12 months, you could place (12)(2) = 24 of the birthdays and not have 3 or more in any given month. However, we have to place 27 birthdays - and if each of the 12 months already has 2 birthdays, then wherever you put those remaining 3 birthdays... there WILL be at least one month that includes at least 3 birthdays. Thus the probability of this outcome is 100% = 1.
Final Answer: E
GMAT assassins aren't born, they're made,
Rich
-
[email protected]
- GMAT Instructor
- Posts: 2630
- Joined: Wed Sep 12, 2012 3:32 pm
- Location: East Bay all the way
- Thanked: 625 times
- Followed by:119 members
- GMAT Score:780
Whenever we see "at least" in a probability question, we want to think about solving the easy way: finding the probability that we DON'T HAVE at least 3 (or whatever), then subtracting that from 1. (We do this because this approach usually simplifies the calculations.)Kaustubhk wrote:Hi Experts,
I'm still confused with the explanations. Can someone please break this down for me?
So if we say, OK, what are the chances that we DON'T have at least 3 students born in the same month, we realize that we then must have AT MOST 2 students born each month.
But there are only 12 months in the year! If we assign 2 students to each month, that's 2 * 12 = 24 birthdays. Now we have 27 students, and only 24 birthdays, so our three remaining students must have been born in SOME MONTH. Whatever month that is already has 2 birthdays in it, so we're forced to have at least three in some month.
-
[email protected]
- GMAT Instructor
- Posts: 2630
- Joined: Wed Sep 12, 2012 3:32 pm
- Location: East Bay all the way
- Thanked: 625 times
- Followed by:119 members
- GMAT Score:780
Here's a visual that might help. Think of the boxes that the pigeons are in as the months. Notice how once we fill the boxes, we still have two pigeons left over. If we want to put those pigeons in a box, that box MUST now contain at least two pigeons, so there MUST be at least one box with at least two pigeons.
In our problem, the boxes are the birth months, and the pigeons are the students.
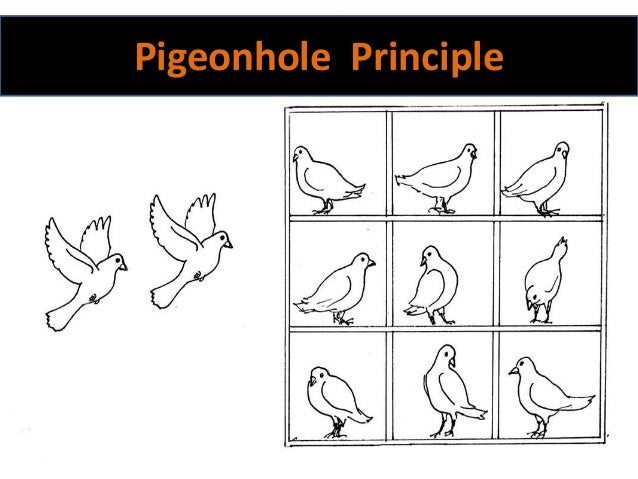
In our problem, the boxes are the birth months, and the pigeons are the students.
-
Mo2men
- Legendary Member
- Posts: 712
- Joined: Fri Sep 25, 2015 4:39 am
- Thanked: 14 times
- Followed by:5 members
Really nice visual explanation.[email protected] wrote:Here's a visual that might help. Think of the boxes that the pigeons are in as the months. Notice how once we fill the boxes, we still have two pigeons left over. If we want to put those pigeons in a box, that box MUST now contain at least two pigeons, so there MUST be at least one box with at least two pigeons.
In our problem, the boxes are the birth months, and the pigeons are the students.
Thanks, Matt
-
[email protected]
- GMAT Instructor
- Posts: 2630
- Joined: Wed Sep 12, 2012 3:32 pm
- Location: East Bay all the way
- Thanked: 625 times
- Followed by:119 members
- GMAT Score:780
If it's still not making sense, check out a few vids on YouTube that explain this concept, which has a great name (the Pigeonhole Principle).
It is absolutely astounding how many applications this has in math, in so many unexpected places. Here are a few (not written by me):
It is absolutely astounding how many applications this has in math, in so many unexpected places. Here are a few (not written by me):
A chess grandmaster has 77 days to prepare for a tournament. He will play at least one game per day, but not more than 132 games in all. Show that there must be some sequence of days in which he plays exactly 21 games
Suppose that n is a positive integer. Show that, for any n, there is a multiple of n whose digits are all either 0 or 5.
If p people attend a party, must there must be at least two attendees with the same number of friends at that party? Why or why not?
I've colored every point in the coordinate plane either blue, green, or red. (It took a while!) Prove that there must be a rectangle somewhere in the plane, all of whose vertices are on points of the same color.
Hi Matt,
Thanks for recommending the videos.
I know the experts have explained but need to type it out here so that i'm clear with my concept.
Explanation: The question is to find the probability that atleast three of them have their birthdays in the same month.
I have taken the complement route. Let's find the probability that there are less then 3 birthdays in a month(atmost 2 birthdays in a month).
12 months --> 27 Students.
12* 2 =24(24 students mapped)
Remaining 3 students have to be mapped in any of the months.This makes our probability zero of ATMOST two birthdays in a month.
The month is not mentioned so it can be any month as RICH mentioned in an earlier post.
So the probability that there will be ATMOST 2 birthdays in a MONTH is ZERO
Hence the probability is 1 (1- 0).
Thanks for recommending the videos.
I know the experts have explained but need to type it out here so that i'm clear with my concept.
Explanation: The question is to find the probability that atleast three of them have their birthdays in the same month.
I have taken the complement route. Let's find the probability that there are less then 3 birthdays in a month(atmost 2 birthdays in a month).
12 months --> 27 Students.
12* 2 =24(24 students mapped)
Remaining 3 students have to be mapped in any of the months.This makes our probability zero of ATMOST two birthdays in a month.
The month is not mentioned so it can be any month as RICH mentioned in an earlier post.
So the probability that there will be ATMOST 2 birthdays in a MONTH is ZERO
Hence the probability is 1 (1- 0).
-
[email protected]
- GMAT Instructor
- Posts: 2630
- Joined: Wed Sep 12, 2012 3:32 pm
- Location: East Bay all the way
- Thanked: 625 times
- Followed by:119 members
- GMAT Score:780
I like it!Kaustubhk wrote:Hi Matt,
Thanks for recommending the videos.
I know the experts have explained but need to type it out here so that i'm clear with my concept.
Explanation: The question is to find the probability that atleast three of them have their birthdays in the same month.
I have taken the complement route. Let's find the probability that there are less then 3 birthdays in a month(atmost 2 birthdays in a month).
12 months --> 27 Students.
12* 2 =24(24 students mapped)
Remaining 3 students have to be mapped in any of the months.This makes our probability zero of ATMOST two birthdays in a month.
The month is not mentioned so it can be any month as RICH mentioned in an earlier post.
So the probability that there will be ATMOST 2 birthdays in a MONTH is ZERO
Hence the probability is 1 (1- 0).
GMAT/MBA Expert
-
[email protected]
- GMAT Instructor
- Posts: 6896
- Joined: Sat Apr 25, 2015 10:56 am
- Location: Los Angeles, CA
- Thanked: 43 times
- Followed by:29 members
Since 27/12 = 2 R 3, that means even if the 27 students’ birth months were equally distributed over 12 months of the year, there must be at least one month with 3 students’ birthdays. Therefore, the probability that at least 3 of them have their birthdays in the same month is 1.
Answer: E
Scott Woodbury-Stewart
Founder and CEO
[email protected]
See why Target Test Prep is rated 5 out of 5 stars on BEAT the GMAT. Read our reviews
