BTGmoderatorDC wrote: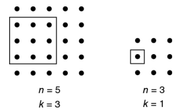
Let n and k be positive integers with k ≤ n. From an n × n array of dots, a k × k array of dots is selected. The figure above shows two examples where the selected k × k array is enclosed in a square. How many pairs (n, k) are possible so that exactly 48 of the dots in the n × n array are NOT in the selected k × k array?
A. 1
B. 2
C. 3
D. 4
E. 5
OA
C
Source: Official Guide
The number of dots in n*n array = n^2, and in those in k*k = k^2, so the dots in the n X n array are NOT in the selected k X k array = n^2 - k^2 = 48, where n > k.
n^2 − k^2 = 48;
(n−k)*(n+k) = 48, since the product 48 is even, at least one of n-k or n+k must be even. Moreover, both n-k or n+k must be even, else if one is even and the other is odd, then n and k will not be positive integers. For example: Say (n−k)*(n+k) = 48 = 1*48. Then n - k = 1 and n + k = 48 => n = 24.5, not a psotive integer
So, 48 can be written as a product of two even numbers as (2, 24); (4, 12); and (6, 8). There are three pairs.
The correct answer:
C
Hope this helps!
-Jay
_________________
Manhattan Review GRE Prep
Locations:
GRE Classes Seattle |
GMAT Prep Course Hong Kong |
GRE Prep San Francisco |
SAT Prep Classes NYC | and many more...
Schedule your free consultation with an experienced GMAT Prep Advisor!
Click here.


















