-
Target Test Prep 20% Off Flash Sale is on! Code: FLASH20
Redeem
Want a 51 on Quant? Answer This Problem!
 Sequence problems arent incredibly common on the test, but if youre doing well on the quant section, be prepared to see one. Now, youve got a choice: do you want to guess quickly and save time for other, easier topics? Do you want to learn some test savvy techniques that will help you with some sequence questions but possibly not all of them? Or do you want to learn how to do these every single time, no matter what?
Sequence problems arent incredibly common on the test, but if youre doing well on the quant section, be prepared to see one. Now, youve got a choice: do you want to guess quickly and save time for other, easier topics? Do you want to learn some test savvy techniques that will help you with some sequence questions but possibly not all of them? Or do you want to learn how to do these every single time, no matter what?
That isnt a trick question. Every good business person knows that theres a point of diminishing returns: if you dont actually need a 51, then you may study for a lower (but still good!) score and re-allocate your valuable time elsewhere.
Try this GMATPrep problem from the free test. After, well talk about how to do it in the textbook way and in the back of the envelope way.
* For every integer k from 1 to 10, inclusive, the kth term of a certain sequence is given by [pmath](-1)^{k+1}(1/2^k)[/pmath]. If T is the sum of the first 10 terms in the sequence, then T is(A) greater than 2
(B) between 1 and 2
(C) between [pmath]1/2[/pmath] and 1
(D) between [pmath]1/4[/pmath]and[pmath]1/2[/pmath]
(E) less than [pmath]1/4[/pmath]
First, lets talk about how to do this thing in the textbook math way. If you dont want to do this the textbook math way, feel free to skip to the second method below.
Textbook Method
If youve really studied sequences, then you may recognize the sequence as a particular kind called a Geometric Progression. If not, you would start to find the terms and see whether you can spot a pattern.
Plug in k = 1, 2, 3. Whats going on?
If k = 1, then[pmath](-1)^{1+1}(1/2^1)=(1)(1/2)=1/2[/pmath]
If k = 2, then[pmath](-1)^{2+1}(1/2^2)=(-1)(1/4)=-1/4[/pmath]
If k = 3, then[pmath](-1)^{3+1}(1/2^3)=(1)(1/8)=1/8[/pmath]
Whats going on here? Each time, the term gets multiplied by [pmath]-1/2[/pmath]in order to get to the next one. When you keep multiplying by the same number in order to get to the next term, then you have a geometric progression.
This next part gets into some serious math. Unless you really just love math, I wouldnt bother learning this part for the GMAT, because theres a very good chance youll never need to use it. But, if you want to, go for it!
When you have a geometric progression, you can calculate the sum in the following way:
[pmath]s=1/2+(-1/4)+1/8+(-1/16)+...[/pmath]
Next, youre going to multiply every term in the sum by the common ratio. Whats the common ratio? Its the constant number that you keep multiplying each term by to get the next one. In this case, youve already figured this out: its [pmath](-1/2)[/pmath].
If you multiply this through all of the terms on both sides of the equation, youll get this:
[pmath](-1/2)s=(-1/4)+1/8+(-1/16)+...[/pmath]
Does anything look familiar? Its basically the same list of numbers as in the first sum equation, except its missing the first number, [pmath]1/2[/pmath]. All of the others are identical!
Subtract this second equation from the first:
[pmath]s-(-1/2)s=1/2[/pmath]
The right-hand side of the equation is always going to be just the first term of the original sum. The rest of the terms on the right-hand side of the two equations are identical, so when you subtract, they become zero and disappear.
Solve for s:
[pmath]{3/2}s=1/2[/pmath]
[pmath]s=1/3[/pmath]
This value falls between 1/4 and 1/2, so the answer is (D).
Back of the Envelope Method
There is another way to tackle this one. At the same time, this problem is really trickyso this solution is still not an easy solution. Your best choice might be just to guess and move on.
Before you start reading the text, take a First Glance at the whole thing. Its a problem-solving problem. The answers are weird. Theyre not exact. What does that mean?
Read the problem, but keep that answer weirdness in mind. The first sentence has a crazy sequence. The question asks you to sum up the first 10 terms of this sequence. And the answers arent exact so apparently you dont need to find the exact sum.
Take a closer look at the form of the answers. Notice anything about them?
They dont overlap! They cover adjacent ranges. If you can figure out that, for example, the sum is about 3/4, then you know the answer must be (C). In other words, you can actually estimate hereyou dont have to do an exact calculation.
That completely changes the way you can approach this problem! Heres the sequence:
[pmath](-1)^{k+1}(1/2^k)[/pmath]
According to the problem, the 10 terms are from k = 1 to k = 10. Calculating all 10 of those and then adding them up is way too much work (another clue that theres got to be a better way to do this one). So what is that better way?
Since you know you can estimate, try to find a pattern. Calculate the first two terms (we had to do this in the first solution, too).
Ifk= 1, then[pmath](-1)^{1+1}(1/2^1)=(1)(1/2)=1/2[/pmath]
Ifk= 2, then[pmath](-1)^{2+1}(1/2^2)=(-1)(1/4)=-1/4[/pmath]
Whats going on? The first answer is positive and the second one is negative. Why? Ah, because the first part of the calculation is -1 raised to a power. That will just keep switching back and forth between 1 and -1, depending on whether the power is odd or even. It wont change the size of the final answer, but it will change the sign.
Okay, and what about that second part? it went from 1/2 to 1/4. What will happen next time? Try just that part of the calculation. If k = 3, then just that part will become [pmath](1/2^3)=1/8[/pmath].
Interesting! So the denominator will keep increasing by a factor of 2: 2, 4, 8, 16 and so on.
Great, now you can write out the 10 numbers!
[pmath]1/2,{-1/4},1/8,{-1/16},1/32,{-1/64}[/pmath] ugh. The denominators getting pretty big. That means the fraction itself is getting pretty small. Do I need to keep writing these out?
What was the problem asking again?
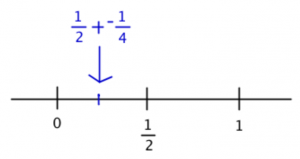
Right, find the sum of these 10 numbers. Lets see. The first number in the sequence is 1/2 and the second is -1/4, so the pair adds up to 1/4.
Right now, the answer would be right between D and E. Does the sum go up or down from here?
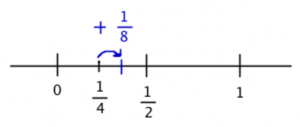
The third number will add 1/8, so it goes up:
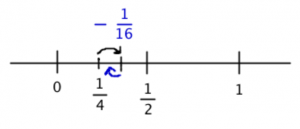
But the fourth will subtract 1/16 (dont forget that every other term is negative!), pulling it back down again:
Hmm. In the third step, it went up but not enough to get all the way to 1/2. Then, it went down again, but by an even smaller amount, so it didnt get all the way back down to 1/4.
The fifth step would go up by an even smaller amount (1/32), and then it would go back down again by yet a smaller number (1/64). What can you conclude?
First, the sum is always growing a little bit, because each positive number is a bit bigger than the following negative number. The sum is never going to drop below 1/4, so cross off answer (E).
You keep adding smaller and smaller amounts, though, so if the first jump of 1/8 wasnt enough to get you up to 1/2, then none of the later, smaller jumps will get you there either, especially because you also keep subtracting small amounts. Youre never going to cross over to 1/2, so the sum has to be between 1/4 and 1/2.
The correct answer is (D).
As I mentioned above, you may decide that you dont want to do this problem at all. These arent that commonmany people wont see one like this on the test. Also, you dont have to get everything right to get a top score. Just last week, I spoke with a student who outright guessed on 4 quant problems, and she still scored a 51 (the top score).
Key Takeaways for Advanced Sequence Problems
(1) Do you even want to learn how to do these? Dont listen to your pride. Listen to your practical side. This might not be the best use of your time.
(2) All of these math problems do have a textbook solution methodbut youd have to learn a lot of math that you might never use if you try to learn all of the textbook methods. Thats not a problem if youre great at math and have a great memory for this stuff. If not
(3) then think about alternate methods that can work just as well. Certain clues will indicate when you can estimate on a problem, rather than solving for the real number. You may already be familiar with some of these, for instance when you see the word approximately in the problem or answer choices that are spread pretty far apart. Now, youve got a new clue to add to your list: answers that offer a range of numbers and the different answer ranges dont overlap.
* GMATPrep questions courtesy of the Graduate Management Admissions Council. Usage of this question does not imply endorsement by GMAC.
Recent Articles
Archive
- April 2024
- March 2024
- February 2024
- January 2024
- December 2023
- November 2023
- October 2023
- September 2023
- July 2023
- June 2023
- May 2023
- April 2023
- March 2023
- February 2023
- January 2023
- December 2022
- November 2022
- October 2022
- September 2022
- August 2022
- July 2022
- June 2022
- May 2022
- April 2022
- March 2022
- February 2022
- January 2022
- December 2021
- November 2021
- October 2021
- September 2021
- August 2021
- July 2021
- June 2021
- May 2021
- April 2021
- March 2021
- February 2021
- January 2021
- December 2020
- November 2020
- October 2020
- September 2020
- August 2020
- July 2020
- June 2020
- May 2020
- April 2020
- March 2020
- February 2020
- January 2020
- December 2019
- November 2019
- October 2019
- September 2019
- August 2019
- July 2019
- June 2019
- May 2019
- April 2019
- March 2019
- February 2019
- January 2019
- December 2018
- November 2018
- October 2018
- September 2018
- August 2018
- July 2018
- June 2018
- May 2018
- April 2018
- March 2018
- February 2018
- January 2018
- December 2017
- November 2017
- October 2017
- September 2017
- August 2017
- July 2017
- June 2017
- May 2017
- April 2017
- March 2017
- February 2017
- January 2017
- December 2016
- November 2016
- October 2016
- September 2016
- August 2016
- July 2016
- June 2016
- May 2016
- April 2016
- March 2016
- February 2016
- January 2016
- December 2015
- November 2015
- October 2015
- September 2015
- August 2015
- July 2015
- June 2015
- May 2015
- April 2015
- March 2015
- February 2015
- January 2015
- December 2014
- November 2014
- October 2014
- September 2014
- August 2014
- July 2014
- June 2014
- May 2014
- April 2014
- March 2014
- February 2014
- January 2014
- December 2013
- November 2013
- October 2013
- September 2013
- August 2013
- July 2013
- June 2013
- May 2013
- April 2013
- March 2013
- February 2013
- January 2013
- December 2012
- November 2012
- October 2012
- September 2012
- August 2012
- July 2012
- June 2012
- May 2012
- April 2012
- March 2012
- February 2012
- January 2012
- December 2011
- November 2011
- October 2011
- September 2011
- August 2011
- July 2011
- June 2011
- May 2011
- April 2011
- March 2011
- February 2011
- January 2011
- December 2010
- November 2010
- October 2010
- September 2010
- August 2010
- July 2010
- June 2010
- May 2010
- April 2010
- March 2010
- February 2010
- January 2010
- December 2009
- November 2009
- October 2009
- September 2009
- August 2009