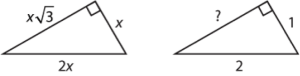-
Target Test Prep 20% Off Flash Sale is on! Code: FLASH20
Redeem
Tackling Multishape Geometry on the GMAT
 What do you do when you realize a geometry problem has just popped up on the screen?
What do you do when you realize a geometry problem has just popped up on the screen?
Try this GMATPrep problem from the free practice test and then well talk about what to do!
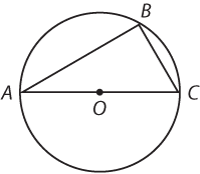
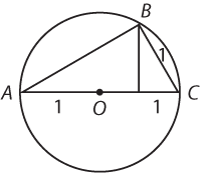
* In the figure above, the radius of the circle with center O is 1 and BC = 1. What is the area of triangular region ABC?
(A) [pmath]sqrt{2}/2[/pmath]
(B)[pmath]sqrt{3}/2[/pmath]
(C) 1
(D)[pmath]sqrt{2}[/pmath]
(E) [pmath]sqrt{3}[/pmath]
Whats your first step? Lets use this problem as an opportunity to practice the Quant Process.
At a glance, you can see that the problem provides a diagram. Draw! Make it big enough that you can add labels as you calculate new pieces of information (and, of course, jot down any information given in the problem).
Finally, write down any formulas youll need, as well as whatever the problem asks you to find. Your scrap paper might look something like this:
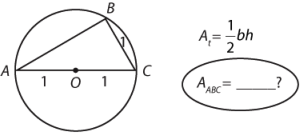
The problem asks for the area of the triangle. You need a base and a height in order to calculate this. You know one possible base: AC = 2. If you draw a vertical line down from B to the base, that would be the corresponding height.
Before you dive in and try to find this height, though, Reflect! Ask yourself whether there are other possible ways to move forward. Sometimes, the obvious way turns out not to be the easiest way to proceed.
In particular, this is a multi-shape problem: you were given both a triangle and a circle. Why did they include the circle? Pay particular attention to where the two shapes overlap.
Hmm. The hypotenuse of the triangle is also a diameter of the circle. How can you use that to solve?
It turns out that when a triangle is inscribed in a circle (the 3 vertices of the triangle all sit on the circle), and the hypotenuse of that triangle is also a diameter of the circle, then the triangle in question is a right triangle. (This is one of the rules were supposed to memorize for the test.)
In this case, the right angle is labeled B. Is that information useful at all? Well, if youre trying to find the area of a right triangle, then you just need to know the lengths of the two legs: AB and BC. The problem says that BC = 1, so the only unknown is AB.
Now you have a choice: do you think itll be easier to find the length of AB or to find the length of the vertical line that you drew in below point B?
Because ABC is a right triangle, its easier to find AB. The short leg is 1 and the hypotenuse is 2. Do those numbers match any of the smart triangles that youve studied? (If not, use the Pythagorean Theorem.)
Yes! These match the 30-60-90 triangle parameters.
The length of AB is [pmath]sqrt{3}[/pmath]. Plug this into the area formula:
[pmath]A={1/2}(sqrt{3})(1)[/pmath]
[pmath]A=sqrt{3}/2[/pmath]
The correct answer is (B).
Key Takeaways for Multishape Geometry.
(1) Examine the overlap between the shapes. Most likely, some rule about that connection exists and this rule will help make the problem easier to solve.
(2) Draw! This is key for any geometry problem, but especially so for multi-shape problems. There are too many moving parts; you need to keep track of everything in a clear way.
(3) Remember our Quant Process: Reflect before you Work! In this case, the first, more obvious path would have been a lot more difficult to execute. Reflecting for a moment allowed you to notice the connection between the circle and the triangle. The subsequent solution path turned out to be much more straightforward.
* GMATPrep questions courtesy of the Graduate Management Admissions Council. Usage of this question does not imply endorsement by GMAC.
Recent Articles
Archive
- April 2024
- March 2024
- February 2024
- January 2024
- December 2023
- November 2023
- October 2023
- September 2023
- July 2023
- June 2023
- May 2023
- April 2023
- March 2023
- February 2023
- January 2023
- December 2022
- November 2022
- October 2022
- September 2022
- August 2022
- July 2022
- June 2022
- May 2022
- April 2022
- March 2022
- February 2022
- January 2022
- December 2021
- November 2021
- October 2021
- September 2021
- August 2021
- July 2021
- June 2021
- May 2021
- April 2021
- March 2021
- February 2021
- January 2021
- December 2020
- November 2020
- October 2020
- September 2020
- August 2020
- July 2020
- June 2020
- May 2020
- April 2020
- March 2020
- February 2020
- January 2020
- December 2019
- November 2019
- October 2019
- September 2019
- August 2019
- July 2019
- June 2019
- May 2019
- April 2019
- March 2019
- February 2019
- January 2019
- December 2018
- November 2018
- October 2018
- September 2018
- August 2018
- July 2018
- June 2018
- May 2018
- April 2018
- March 2018
- February 2018
- January 2018
- December 2017
- November 2017
- October 2017
- September 2017
- August 2017
- July 2017
- June 2017
- May 2017
- April 2017
- March 2017
- February 2017
- January 2017
- December 2016
- November 2016
- October 2016
- September 2016
- August 2016
- July 2016
- June 2016
- May 2016
- April 2016
- March 2016
- February 2016
- January 2016
- December 2015
- November 2015
- October 2015
- September 2015
- August 2015
- July 2015
- June 2015
- May 2015
- April 2015
- March 2015
- February 2015
- January 2015
- December 2014
- November 2014
- October 2014
- September 2014
- August 2014
- July 2014
- June 2014
- May 2014
- April 2014
- March 2014
- February 2014
- January 2014
- December 2013
- November 2013
- October 2013
- September 2013
- August 2013
- July 2013
- June 2013
- May 2013
- April 2013
- March 2013
- February 2013
- January 2013
- December 2012
- November 2012
- October 2012
- September 2012
- August 2012
- July 2012
- June 2012
- May 2012
- April 2012
- March 2012
- February 2012
- January 2012
- December 2011
- November 2011
- October 2011
- September 2011
- August 2011
- July 2011
- June 2011
- May 2011
- April 2011
- March 2011
- February 2011
- January 2011
- December 2010
- November 2010
- October 2010
- September 2010
- August 2010
- July 2010
- June 2010
- May 2010
- April 2010
- March 2010
- February 2010
- January 2010
- December 2009
- November 2009
- October 2009
- September 2009
- August 2009