Data Sufficiency

siddhu161 wrote:What is the volume of a certain rectangular solid?

1. Two adjacent faces have areas 15 and 24.
2. Each of two opposite faces of the solid has area 40.

This is OG question.

The problem I am facing is understanding second statement.
Can anyone please help in understanding the meaning?

Two opposite faces of rectangular solid will always have same area. So does this statement mean that all 3 pairs of opposite faces have same areas?

Please help.

Target question: What is the volume of a certain rectangular solid?

Aside: A rectangular solid is a box

Statement 1: Two adjacent faces of the solid have areas 15 and 24, respectively.
There are several different rectangular solids that meet this condition. Here are two:
Case a: the dimensions are 1x15x24, in which case the volume is 360
Case b: the dimensions are 3x5x8, in which case the volume is 120
Since we cannot answer the target question with certainty, statement 1 is NOT SUFFICIENT

Statement 2: Each of two opposite faces of the solid has area 40.
So, there are two opposite faces that each have area 40.
Definitely NOT SUFFICIENT

Statements 1 and 2 combined:
So, we know the area of each face (noted in blue on the diagram below).
Let's let x equal the length of one side.



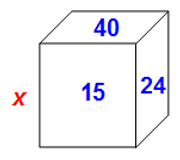
Since the area of each face = (length)(width), we can express the other two dimensions in terms of x.


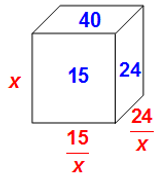
From here, we'll focus on the face that has area 40.
This face has dimensions (15/x) by (24/x)
Since the area is 40, we know that (15/x)(24/x) = 40
Expand: 360/(x^2) = 40
Simplify: 360 = 40x^2
Simplify: 9 = x^2
Solve: x = 3 or -3
Since the side lengths must be positive, we can be certain that x = 3

When we plug x=3 into the other two dimensions, we get 15/3 and 24/3
So, the 3 dimensions are 3, 5, and 8, which means the volume of the rectangular solid must be 120.
Since we can answer the target question with certainty, the combined statements are SUFFICIENT

Answer: C

Cheers,
Brent

siddhu161 wrote:Thanks Brent,

My problem was only understanding 2nd statement.
It's kinda confusing if read separately.

Although, we should not consider 1st statement while reading 2nd, for this particular question it is somehow happening.

If you consider 2nd statement independently,

suppose 3 sides of length a,b,c.
then ab = bc = ac = 40. --> (a^2)(b^2)(c^2) = 64000 --> volume = abc = sqrt(64000) hence the answer.

Due to this I am getting confused.

The above scenario, ab = bc = ac = 40, is one possible scenario that meets the conditions in statement 2. In this possible scenario, the area = √64000
Now, if that were THE ONLY scenario that met the conditions in statement 2, then statement 2 would be sufficient.
However, there are other scenarios as well. For example, the measurements could also be 3x5x8 (in which case two opposite faces would each have area 40). In this possible scenario, the area = 120

Since our two possible scenarios yield different volumes, statement 2 must be INSUFFICIENT.

Cheers,
Brent

I think you're reading statement 2 as "ANY two opposite faces will each have area 40," when the statement really tells us that there happen to be at least 2 opposite faces with area 40 each.

Cheers,
Brent