BTGmoderatorLU wrote: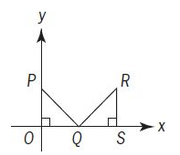
In the rectangular coordinate system above, if ΔOPQ and ΔQRS have equal area, what are the coordinates of point R?
(1) The coordinates of point P are (0, 12).
(2) OP = OQ and QS = RS.
Statement 1:
Thus, OP=12.
Case 1: OQ=1, QS=1, and RS=12, with the result that the area of reach triangle = (1/2)(1)(12) = 6
In this case, R = (2, 12).
Case 2: OQ=1, QS=12, and RS=1, with the result that the area of reach triangle = (1/2)(1)(12) = 6
In this case, R = (13, 1).
Since R can have different coordinates, INSUFFICIENT.
INSUFFICIENT.
Statement 2:
Since both triangles are isosceles right triangles and have equal areas, all four legs must be equal:
OP=OQ=QS=RS.
Case 3: OP=OQ=QS=RS=12, with the result that the area of each triangle = (1/2)(12)(12) = 72
In this case, R = (24, 12).
Case 4: OP=OQ=QS=RS=2, with the result that the area of each triangle = (1/2)(2)(2) = 2
In this case, R = (4, 2).
Since R can have different coordinates, INSUFFICIENT.
Statements combined:
Since OP=12 and OP=OQ=QS=RS, only Case 3 is possible:
OP=OQ=QR=RS=12.
Thus, R = (24, 12).
SUFFICIENT.
The correct answer is
C.
Private tutor exclusively for the GMAT and GRE, with over 20 years of experience.
Followed here and elsewhere by over 1900 test-takers.
I have worked with students based in the US, Australia, Taiwan, China, Tajikistan, Kuwait, Saudi Arabia -- a long list of countries.
My students have been admitted to HBS, CBS, Tuck, Yale, Stern, Fuqua -- a long list of top programs.
As a tutor, I don't simply teach you how I would approach problems.
I unlock the best way for YOU to solve problems.
For more information, please email me (Mitch Hunt) at
[email protected].
Student Review #1
Student Review #2
Student Review #3