BREAKING: Target Test Prep releases Brand New 2026 On Demand GMAT prep course

Redeem

If rectangle ABCD is inscribed in the circle above, what is

This topic has expert replies
Post new topic Post Reply
Previous Topic Next Topic
Master | Next Rank: 500 Posts
Posts: 394
Joined: Sun Jul 02, 2017 10:59 am
Thanked: 1 times
Followed by:5 members

If rectangle ABCD is inscribed in the circle above, what is

by AbeNeedsAnswers » Fri May 03, 2019 5:54 pm

Timer

00:00

Your Answer

A

B

C

D

E

Global Stats

Image

If rectangle ABCD is inscribed in the circle above, what is the area of the circular region?

A) 36.00Ï€
B) 42.25Ï€
C) 64.00Ï€
D) 84.50Ï€
E) 169.00Ï€

B

Source: Official Guide 2020
Top
Source: — Problem Solving |

GMAT/MBA Expert

User avatar
GMAT Instructor
Posts: 16207
Joined: Mon Dec 08, 2008 6:26 pm
Location: Vancouver, BC
Thanked: 5254 times
Followed by:1268 members
GMAT Score:770

by Brent@GMATPrepNow » Sat May 04, 2019 6:01 am
AbeNeedsAnswers wrote: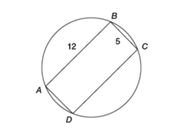Image

If rectangle ABCD is inscribed in the circle above, what is the area of the circular region?

A) 36.00Ï€
B) 42.25Ï€
C) 64.00Ï€
D) 84.50Ï€
E) 169.00Ï€

B

Source: Official Guide 2020
Draw a line connecting points A and C.
Image
An important circle property (see video below for more info) tells us that, if we have a 90-degree inscribed angle, then that angle must be containing ("holding") the DIAMETER of the circle.
So, we know that AC = the diameter of the circle.


To find the hypotenuse of the red triangle, we can EITHER apply the Pythagorean Theorem OR recognize that 5 and 12 are part of the Pythagorean triplet 5-12-13
Image
With either approach, we learn that AC = 13

IMPORTANT: if the diameter (AC) is 13, then the radius = 13/2 = 6.5

What is the area of the circular region?
Area of circle = πr²
So, area = π(6.5²)
= 42.25Ï€

Answer: B

Cheers,
Brent
Brent Hanneson - Creator of GMATPrepNow.com
Image
Top
Legendary Member
Posts: 2499
Joined: Sun Oct 29, 2017 2:04 pm
Followed by:6 members

by swerve » Sat May 04, 2019 10:36 am
The rectangle is equally placed on the center of the circle.

Let \(O\) be the center of the circle.

And \(X\) be the midpoint of \(AB\).

Then \(OX = \frac{5}{2} \) and \(XB = \frac{12}{2} = 6\)

Triangle \(OXB\) is a right angles triangle.

\(OB = radius = \sqrt{6^2+2.5^2}=\sqrt{42.5}\)

Area \(= \pi \cdot r^2 = 42.5\pi\)

Hence, __B__
Top

GMAT/MBA Expert

User avatar
Elite Legendary Member
Posts: 10392
Joined: Sun Jun 23, 2013 6:38 pm
Location: Palo Alto, CA
Thanked: 2867 times
Followed by:511 members
GMAT Score:800

by [email protected] » Wed May 22, 2019 8:46 am
Hi All,

We're told that a rectangle with sides of 5 and 12 is inscribed in the circle. We're asked for the area of the circular region. This question is based on a number of math patterns that can help you to save time answering the question.

First, any square or rectangle that is inscribed in a circle will have a diagonal that IS the diameter of the circle. Second, when splitting a rectangle or square across its diagonal, you'll form two right triangles. With the given side lengths of the rectangle (5 and 12), we have a 5/12/13 right triangle, so we know the diameter of the circle is 13. The radius is half the diameter... radius = 6.5

Area of a circle = (Ï€)(R^2) = (Ï€)(6.5^2)

At this point, you don't actually have to calculate the value. Since 6^2 = 36 and 7^2 = 49, we know the correct answer has to be between 36Ï€ and 49Ï€. There's only one answer that fits...

Final Answer: B

GMAT assassins aren't born, they're made,
Rich
Contact Rich at [email protected]
Image
Top
Post new topic Post Reply
• Page 1 of 1