A rectangular frame has a length of 18 inches and width of 15 inches. The frame encloses a rectangular picture that has the same area as the frame itself. If the length and width of the picture have the same ratio as the length and width of the frame, what is the length of the picture, in inches?
(A) 9 * sqrt2
(B) 3/2
(C) 9/sqrt2
(D) 15*(1-1/sqrt2)
(E) 9/2
OA is A.
Source- GMAT Practice Set
Length of a Rectangle
This topic has expert replies
-
pareekbharat86
- Master | Next Rank: 500 Posts
- Posts: 168
- Joined: Thu Nov 01, 2012 7:43 pm
- Thanked: 1 times
GMAT/MBA Expert
- Brent@GMATPrepNow
- GMAT Instructor
- Posts: 16207
- Joined: Mon Dec 08, 2008 6:26 pm
- Location: Vancouver, BC
- Thanked: 5254 times
- Followed by:1268 members
- GMAT Score:770
So, we have something like thispareekbharat86 wrote:A rectangular frame has a length of 18 inches and width of 15 inches. The frame encloses a rectangular picture that has the same area as the frame itself. If the length and width of the picture have the same ratio as the length and width of the frame, what is the length of the picture, in inches?
(A) 9√2
(B) 3/2
(C) 9/√2
(D) 15(1- 1/√2)
(E) 9/2
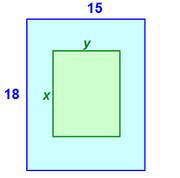
The frame encloses a rectangular picture that has the same area as the frame itself.
The area of the 18 by 15 rectangle = (18)(15) = 270
Half of this area is frame and half is picture.
So, the area of the blue frame = 135, and the area of the green rectangle = 135
In other words, xy = 135
The length and width of the picture have the same ratio as the length and width of the frame
In other words, x/y = 18/15
We can rewrite this as: y = 15x/18
We now have two equations:
xy = 135
y = 15x/18
Take the first equation and replace y with 15x/18 to get...
(x)(15x/18) = 135
Simplify: 15x²/18 = 135
Divide both sides by 15 to get: x²/18 = 9
Multiply both sides by 18 to get: x² = 162
Find square root of both sides to get: x = √162
Simplify: x = (√81)(√2)
Simplify: x = [spoiler]9√2 = A[/spoiler]
Cheers,
Brent
- GMATGuruNY
- GMAT Instructor
- Posts: 15539
- Joined: Tue May 25, 2010 12:04 pm
- Location: New York, NY
- Thanked: 13060 times
- Followed by:1906 members
- GMAT Score:790
The frame encloses a rectangular picture that has the same area as the frame itself.pareekbharat86 wrote:A rectangular frame has a length of 18 inches and width of 15 inches. The frame encloses a rectangular picture that has the same area as the frame itself. If the length and width of the picture have the same ratio as the length and width of the frame, what is the length of the picture, in inches?
(A) 9 * sqrt2
(B) 3/2
(C) 9/sqrt2
(D) 15*(1-1/sqrt2)
(E) 9/2
Thus, the picture's area is equal to half of the TOTAL area:
(1/2) * 18 * 15 = 135.
The length and width of the picture have the same ratio as the length and width of the frame.
L:W = 18:15 = 6:5 = 12:10.
If L=12 and W=10, then the area of the picture = 12*10 = 120.
Since the actual area is 135 -- a bit more than 120 -- the actual value of L must be a bit more than 12.
Only A works:
9√2 ≈ 9 * 1.4 = 12.6
The correct answer is A.
Private tutor exclusively for the GMAT and GRE, with over 20 years of experience.
Followed here and elsewhere by over 1900 test-takers.
I have worked with students based in the US, Australia, Taiwan, China, Tajikistan, Kuwait, Saudi Arabia -- a long list of countries.
My students have been admitted to HBS, CBS, Tuck, Yale, Stern, Fuqua -- a long list of top programs.
As a tutor, I don't simply teach you how I would approach problems.
I unlock the best way for YOU to solve problems.
For more information, please email me (Mitch Hunt) at [email protected].
Student Review #1
Student Review #2
Student Review #3
Followed here and elsewhere by over 1900 test-takers.
I have worked with students based in the US, Australia, Taiwan, China, Tajikistan, Kuwait, Saudi Arabia -- a long list of countries.
My students have been admitted to HBS, CBS, Tuck, Yale, Stern, Fuqua -- a long list of top programs.
As a tutor, I don't simply teach you how I would approach problems.
I unlock the best way for YOU to solve problems.
For more information, please email me (Mitch Hunt) at [email protected].
Student Review #1
Student Review #2
Student Review #3
Isn't that an incorrect way of framing a question. It says the frame has L =18 W = 15. So, area of frame has to be 18*15. hence the term "area of frame = that of picture" doesn't stand. My question is - In GMAT will questions be asked on similar lines, or it will be specified that area of left over area in the frame = area of the picture ... [confused]GMATGuruNY wrote:The frame encloses a rectangular picture that has the same area as the frame itself.pareekbharat86 wrote:A rectangular frame has a length of 18 inches and width of 15 inches. The frame encloses a rectangular picture that has the same area as the frame itself. If the length and width of the picture have the same ratio as the length and width of the frame, what is the length of the picture, in inches?
(A) 9 * sqrt2
(B) 3/2
(C) 9/sqrt2
(D) 15*(1-1/sqrt2)
(E) 9/2
Thus, the picture's area is equal to half of the TOTAL area:
(1/2) * 18 * 15 = 135.
The length and width of the picture have the same ratio as the length and width of the frame.
L:W = 18:15 = 6:5 = 12:10.
If L=12 and W=10, then the area of the picture = 12*10 = 120.
Since the actual area is 135 -- a bit more than 120 -- the actual value of L must be a bit more than 12.
Only A works:
9√2 ≈ 9 * 1.4 = 12.6
The correct answer is A.
GMAT/MBA Expert
- [email protected]
- Elite Legendary Member
- Posts: 10392
- Joined: Sun Jun 23, 2013 6:38 pm
- Location: Palo Alto, CA
- Thanked: 2867 times
- Followed by:511 members
- GMAT Score:800
Hi fifafreak,
While the frame has dimensions of 18 x 15, that DOES not mean that its area is 18 x 15. It's a frame, so there's a "hole" in it where the picture would go, thus the area of the frame is something LESS THAN 18 x 15.
We're told that the area of the picture = area of the frame. This tells us that the frame area + picture area = 18 x 15.
These types of geometry questions are always specifically worded, so you have to pay careful attention to the details (drawing a picture usually helps), but you won't see that many on the actual GMAT (maybe 1, possibly 0).
GMAT assassins aren't born, they're made,
Rich
While the frame has dimensions of 18 x 15, that DOES not mean that its area is 18 x 15. It's a frame, so there's a "hole" in it where the picture would go, thus the area of the frame is something LESS THAN 18 x 15.
We're told that the area of the picture = area of the frame. This tells us that the frame area + picture area = 18 x 15.
These types of geometry questions are always specifically worded, so you have to pay careful attention to the details (drawing a picture usually helps), but you won't see that many on the actual GMAT (maybe 1, possibly 0).
GMAT assassins aren't born, they're made,
Rich
-
pareekbharat86
- Master | Next Rank: 500 Posts
- Posts: 168
- Joined: Thu Nov 01, 2012 7:43 pm
- Thanked: 1 times
I still don't get it. Why are we halving the area?GMATGuruNY wrote:The frame encloses a rectangular picture that has the same area as the frame itself.pareekbharat86 wrote:A rectangular frame has a length of 18 inches and width of 15 inches. The frame encloses a rectangular picture that has the same area as the frame itself. If the length and width of the picture have the same ratio as the length and width of the frame, what is the length of the picture, in inches?
(A) 9 * sqrt2
(B) 3/2
(C) 9/sqrt2
(D) 15*(1-1/sqrt2)
(E) 9/2
Thus, the picture's area is equal to half of the TOTAL area:
(1/2) * 18 * 15 = 135.
The length and width of the picture have the same ratio as the length and width of the frame.
L:W = 18:15 = 6:5 = 12:10.
If L=12 and W=10, then the area of the picture = 12*10 = 120.
Since the actual area is 135 -- a bit more than 120 -- the actual value of L must be a bit more than 12.
Only A works:
9√2 ≈ 9 * 1.4 = 12.6
The correct answer is A.
Thanks,
Bharat.
Bharat.
GMAT/MBA Expert
- [email protected]
- Elite Legendary Member
- Posts: 10392
- Joined: Sun Jun 23, 2013 6:38 pm
- Location: Palo Alto, CA
- Thanked: 2867 times
- Followed by:511 members
- GMAT Score:800
Hi Bharat,
The question tells us that we have a frame and a picture within the frame. The total area of EVERYTHING is 18in x 15in = 270 sq. inches. We're also told that the frame has the SAME AREA as the picture. In math terms:
Area of Frame = Area of Picture
Area of Frame + Area of Picture = 270
Using substitution, you'll see that each Area = 135. This is HALF of the total (270).
GMAT assassins aren't born, they're made,
Rich
The question tells us that we have a frame and a picture within the frame. The total area of EVERYTHING is 18in x 15in = 270 sq. inches. We're also told that the frame has the SAME AREA as the picture. In math terms:
Area of Frame = Area of Picture
Area of Frame + Area of Picture = 270
Using substitution, you'll see that each Area = 135. This is HALF of the total (270).
GMAT assassins aren't born, they're made,
Rich
-
pareekbharat86
- Master | Next Rank: 500 Posts
- Posts: 168
- Joined: Thu Nov 01, 2012 7:43 pm
- Thanked: 1 times
Hi Rich.C,[email protected] wrote:Hi Bharat,
The question tells us that we have a frame and a picture within the frame. The total area of EVERYTHING is 18in x 15in = 270 sq. inches. We're also told that the frame has the SAME AREA as the picture. In math terms:
Area of Frame = Area of Picture
Area of Frame + Area of Picture = 270
Using substitution, you'll see that each Area = 135. This is HALF of the total (270).
GMAT assassins aren't born, they're made,
Rich
Thanks for the explanation. I could have never been able to interpret that Area of Frame+Area of Picture= 270. Its certainly not a straight forward question. Thanks again.
Thanks,
Bharat.
Bharat.
-
Zach.J.Dragone
- Junior | Next Rank: 30 Posts
- Posts: 29
- Joined: Wed Nov 20, 2013 5:35 pm
- Thanked: 1 times
I know this may be stupid but:
We now have two equations:
xy = 135
y = 15x/18
Why is that? In other words, why do we set up the equation with those numbers? I see where they come from but I don't know why we use them. Why can't we set up the frame equation as 6x*5y=135?
We now have two equations:
xy = 135
y = 15x/18
Why is that? In other words, why do we set up the equation with those numbers? I see where they come from but I don't know why we use them. Why can't we set up the frame equation as 6x*5y=135?




















