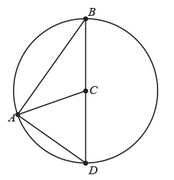
Statement 1
The ratio of the area of the region enclosed by segment AC, segment CB and minor arc AB to the area of triangle ABC is equal to ratio of half the area of circle to the area of triangle ABD.
A, B, C, and D are areas of the region as shown in the question, hence
$$\frac{\left(a+b\right)}{b}=\frac{\left(a+b+c+d\right)}{\left(b+c\right)}$$
$$ab+ac+b^2+bc=ab+b^2+bc+bd$$
$$ac=bd$$
Areas b and c has same base radius, r (radius) and height is the same, so b = c and ac = ad or a = d
since a = d and b = c , we can say that a+b = c+d
This is possible only if AC divides the semicircle in equal parts and thus ABD is isosceles right angled triangle.
$$AB=AD=\frac{BD}{\sqrt{2}}=\frac{2r}{\sqrt{2}}=r\sqrt{2}$$
But we don't have any information on r, hence statement 1 is INSUFFICIENT.
Statement 2
The ratio of the perimeter of triangle ABC to the area of triangle ACD is
$$\left(2+\sqrt{2}\right):6$$
$$we\ can\ say\ that\ \ \frac{\left(AB+BC+AC\right)}{C}=\frac{\left(2+\sqrt{2}\right)}{6}$$
$$\frac{\left(AB+r+r\right)}{C}=\frac{\left(2+\sqrt{2}\right)}{6},\ no\ interaction\ about\ the\ value\ of\ r\ $$
Hence Statement 2 is INSUFFICIENT.
Combining statement 1 and 2 together
$$\frac{\left(AB+2r\right)}{C}=\frac{\left(2+\sqrt{2}\right)}{6}$$
$$\frac{\left(r\sqrt{2}+2r\right)}{\frac{1}{2}\cdot AD\cdot BD}=\frac{\left(2+\sqrt{2}\right)}{6}$$
$$\frac{r\left(2+\sqrt{2}\right)}{\frac{1}{2}\cdot r\cdot r}=\frac{\left(2+\sqrt{2}\right)}{6}=\frac{1}{2}\cdot r=6,\ and\ r=12$$
$$area=\pi r^2=\pi\cdot12^2=144\pi\ $$
$$Two\ statements\ are\ SUFFICIENT\ \ $$
$$answer\ is\ Option\ C$$