Problem Solving

KylieAquino87 wrote:Hi there,

So I realize this post is super old, but I've just began preparing myself for to take the GMAT in 2014 and Quant is what I most need to focus on. Is there anyone who might be able to explain the rationale behind these calculations to me in a way that a person without extensive Quant background could understand?

Thanks a million in advance!

Hi KylieAquino87,

Before providing a solution, I should point out that this is a very tricky question (700+). So, only those in the top 5% (perhaps even top 1%) would ever see such a question.

I just replaced my original solution with a very detailed step-by-step solution.
I'll repost it here as well:

Here's my full solution:

First recognize that we need to choose 3 of the following 9 points to create a triangle.


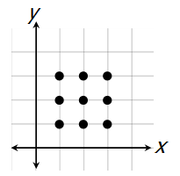
So, for example, if we choose these three points...

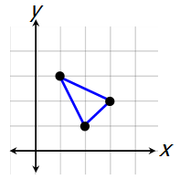
...we get this triangle.

Likewise, if we choose these three points...

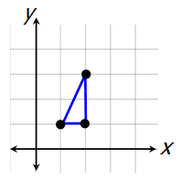
...we get this triangle.

So, the question really comes down to "In how many ways can we select 3 of the 9 points?"
Well, notice that the order of the 3 selected points does not matter. In other words, selecting the points (1,2), (1,3) and (3,2) will create the SAME TRIANGLE as selecting the points (3,2), (1,3) and (1,2).
Since the order of the selected points does not matter, we can use combinations.

We can select 3 points from 9 points in 9C3 ways ( = 84 ways)

Aside: If anyone is interested, we have a free video on calculating combinations (like 9C3) in your head: https://www.gmatprepnow.com/module/gmat-counting?id=789

Now, unfortunately, the correct answer is not 84, because not every selection of 3 points will yield a triangle. For example, if we select these 3 points...

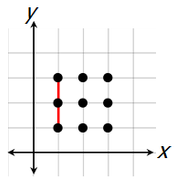
...we get a straight line, NOT a triangle.

So, we must subtract from 84 all of the 3-point selections that DO NOT yield triangles.

To begin, if the 3 selected points are lined up vertically...

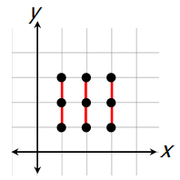
...then we don't get a triangle.
There are 3 different ways to select three points to create a vertical line.

Also, if the 3 selected points are lined up horizontally...

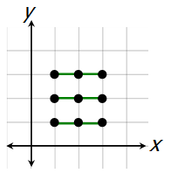
...then we don't get a triangle.
There are 3 different ways to select three points to create a horizontal line.

Finally, if the 3 selected points are lined up diagonally...

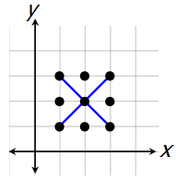
...then we don't get a triangle.
There are 2 different ways to select three points to create a diagonal line.

So, the total number of different triangles = 84 - 3 - 3 - 2
= 76
= B

Cheers,
Brent

verma.kumarrishikesh wrote:Brent thank you for graphical solution it really reduces time.
to find exceptions I was working with y=mx+c check which took a lot of time finding the last diagnol line hence approach was wrong.

(x,y) vertices are integers with conditions 1<=x<=3, 1<=y<=3
so over all we get 9 coordinates with arrangement of 123 for x and y respectively
(1,1)(2,1)(3,1)(2,1)(2,2)(2,3)(3,1)(3,2)(3,3)- 9 set of coordinates of x and y

if we define construction of triangle as a selection of 3 points

Stage 1- Selection of Point A
Stage 2- Selection Of Point B
Stage 3- Selection of Point C

Now Order of Selection of points does not matter hence a combination problem.

So no of selecting 3 coordinates out of 9 is 9c3= 84

But for Triangle all three points cannot be on the same line so exceptions are

Case 1-(1,1) (1,2) (1,3)- Parallel to X axis
Case 2-(2,1) (2,2) (2,3)- Parallel to X axis
Case 3-(3,1) (3,2) (3,3)- Parallel to X axis
Case 4-(1,1) (2,1) (2,1)- Parallel to y Axis
Case 5-(1,2) (2,2) (3,2)- Parallel to y Axis
Case 6-(1,3) (2,3) (3,3)- Parallel to y Axis
Case 7-(1,1) (2,2) (3,3)- 1st diagnol line ( slop is same =1, c=0)
now the tough part
(1,3)(2,2)(3,1)- 2nd diagnol line ( slope is -1 and c=4 in equation y=mx+c)

hence total triangles = 84-8=76

Nice work. You got 84 (9c3) quickly.
Once you recognized that we needed to eliminate some of those 84 selections, a sketch would have been useful.

Cheers,
Brent

lulufrenchie wrote:I totally freak out when I see this kind of questions. I have no idea what to do.

Do you have any tips for this question ?

Brent gave a really good explanation and it looks really easy when you have it. But how do you get there ?

Thanks in advance.

Hey lulufrenchie,

First off, this is a difficult question (I'd say around the 700 level), so don't worry too much about it.
That said, we do have a counting question, so we might first take stock of the various counting techniques we have in our "toolbox"
We might consider LISTING (drawing) all of the possible triangles, but the relatively large answer choices should dissuade us from this approach.

So, what else can we do?
Well, we know that (for the most part) any three points will create a triangle. So, let's go from there.
In how many ways can we select 3 of the 9 points?
Since the order of the selected points doesn't matter, we can use combinations.
We can select 3 points from 9 points in 9C3 ways (84 ways)

At this point, we need to recognize that NOT ALL sets of 3 points will create a triangle. So, we must subtract from 84 all of the 3-point selections that DON'T yield a triangle.
As you can see from the various solutions, there are 8 such 3-point solutions.

So, we get 84 - 8 = 76

Cheers,
Brent

ameraz wrote:

rajs2010 wrote:

rajs2010 wrote:

[email protected] wrote:I do not understand the logic behind these Daily GMAT Questions. The questions are only being answered by other students and never given a confirmed correct answer. If this is really the case, continuing in these discussions would be like the Blind Leading the Blind. Will the instructor giving these questions out ever give the correct answer?

I agree..I subscribed to the daily questions yesterday and got the very first email today....It'll be really helpful if the correct answer is published too, with these daily questions...

If the idea is to promote some healthy discussion first on these questions to explore all the possible ways one could go wrong,it might be a good idea to have the correct answer by the Moderator/Expert in next days email...

I just joined today too and I believe the correct answer is given in the 3 post by the GMATPrept Instructor posted Wed Jan 21, 2009 8:29 pm.

As ameraz points out, the correct answer is given in the 3rd post. That said, I went back and added the official answer to the original question.

Cheers,
Brent

[email protected] wrote:What is the correct answer? lots of confusion by different replies.

The correct answer is provided on the first post, where it says "Answer: B"

Cheers,
Brent