Problem Solving

sachin_yadav wrote:|x² - 5x| < 6
My approach:- -6 < x² - 5x < 6

There are two inequalities:-
(a) x² - 5x < 6
--> x² - 5x - 6 < 0
--> I am stuck over here

(b) x² - 5x > -6
--> x² - 3x - 2x + 6 > 0
--> x(x - 3) - 2(x - 3) > 0
--> (x - 3) and (x - 2) > 0
--> x = 3 and x = 2
--> x > 3 and x < 2 (not sure if it is correct)

You're correct about the two inequality part.
Let me show how to solve them,
(a) x² - 5x - 6 < 0
--> x² - 6x + x - 6 < 0
--> x(x - 6) + (x - 6) < 0
--> (x + 1)(x - 6) < 0
--> Either {(x + 1) > 0 and (x - 6) < 0} or {(x + 1) < 0 and (x - 6) > 0}
--> Either {x > -1 and x < 6} or {x < -1 and x > 6}
--> As the second set is not possible for any x, our final solution is {x > -1 and x < 6}, i.e. -1 < x < 6

(b) x² - 5x > -6
--> x² - 3x - 2x + 6 > 0
--> x(x - 3) - 2(x - 3) > 0
--> (x - 2)(x - 3) > 0
--> Either {(x - 2) > 0 and (x - 3) > 0} or {(x - 2) < 0 and (x - 3) < 0}
--> Either {x > 2 and x > 3} or {x < 2 and x < 3}
--> Either x > 3 or x < 2

Hence, together our final solution : -1 < x < 6 AND {x < 2 or x > 3} ---> -1 < x < 2 OR 3 < x < 6

Note : It is very much unlikely that you'll see absolute value problems like this in GMAT. Most absolute value problems in GMAT can be solved by the concept of distance on the number line or minimal algebra.

This problem can solved easily with wavy curve method too (Read here : https://www.beatthegmat.com/gmat-prep-ea ... tml#602154)

Draw the wavy curves of (a) and (b) as follows,

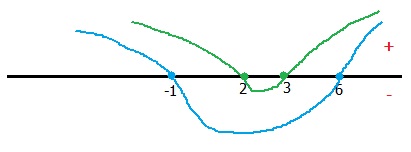
(a) --> Blue
(b) --> Green

Now their solution regions are as follows,

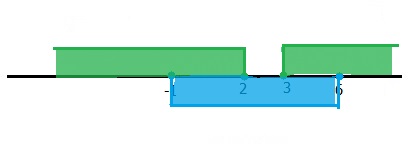
Hence, the final solution for x is where the green and blue regions overlap, i.e. -1 < x < 2 or 3 < x < 6

sachin_yadav wrote:(2). |x² - 2x| < x

Note that, |x² - 2x| is a positive quantity as absolute value cannot be negative and if x = 0, the inequality will not hold. Hence, x > |x² - 2x| > 0 --> x > 0 (Remember this as I won't consider negative values of x anymore.)

Now, |x² - 2x| = |x(x - 2)|
As x > 0, the value of |x² - 2x| depends upon whether (x - 2) > 0 or not

Case #1 : 0 < x < 2

• (x - 2) < 0 ---> x(x - 2) < 0 ---> |x² - 2x| = -x(x - 2) = -(x² - 2x)
  So, -(x² - 2x) < x
  --> x² - 2x + x > 0
  --> x² - x > 0
  --> x(x - 1) > 0
  --> x > 0 and x > 1
  --> x > 1
  So, final solution, 1 < x < 2

Case #2 : x > 2

• (x - 2) > 0 ---> x(x - 2) > 0 ---> |x² - 2x| = x(x - 2) = (x² - 2x)
  So, (x² - 2x) < x
  --> x² - 2x - x < 0
  --> x² - 3x < 0
  --> x(x - 3) < 0
  --> x > 0 and x < 3
  --> x < 3
  So, final solution, 2 < x < 3

Our final solution : 1 < x < 2 or 2 < x < 3 ---> 1 < x < 3 excluding 2