Problem Solving

[GMAT math practice question]

The following figure shows line l: y = 2x. If the area of BOC is 8, what is the area of triangle AOB?

A. 4
B. 6
C. 8
D. 11
E. 13

=>

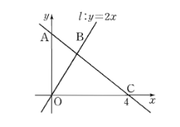
Since the area of the triangle OBC is 8 and the length of the base OC is 4, and the area of a triangle = 1/2bh, we have:
8 = 1/2(4)h
8 = 2h
h = 4.

The height of the triangle is 4, and the y-coordinate of point B is 4.
Since point B is on the line y = 2x, we have 4 = 2x or x = 2.
Then we have point B(2, 4).

We can then determine the equation of the line passing through B (2, 4) and C (4, 0). We first determine the slope of the line using the equation
(y1 - y2) / (x1 - x2)
(4 - 0) / (2 - 4)
4 / -2
Slope = m = -2.

Then, using the point (4, 0) and m = 4 we get:
y = mx + b
0 = -2(4) + b
b = 8

The line passing through B and C is y = -2x + 8.

Point A has an x-coordinate of 0, so y = -2(0) + 9, or y = 8.
Then we have point A(0,8).

The triangle AOB has base OA = 8, and the height equals 2 since the x-coordinate of B is 2. Then the area of triangle OAB is (1/2)*8*2 = 8.

Therefore, C is the answer.
Answer: C