A certain square is to be drawn on a coordinate plane. One of the vertices must be on the origin, and the square is to have an area of 100. If all coordinates of the vertices must be integers, how many different ways can this square be drawn?
A. 4
B. 6
C. 8
D. 10
E. 12
5-Day Free Trial
5-day free, full-access trial TTP
Available with Beat the GMAT members only code
MORE DETAILS
Coordinate/P&C
This topic has expert replies
-
Matt@VeritasPrep
- GMAT Instructor
- Posts: 2630
- Joined: Wed Sep 12, 2012 3:32 pm
- Location: East Bay all the way
- Thanked: 625 times
- Followed by:119 members
- GMAT Score:780
Since the side of the square must have length 10, there must be a line of length 10 from the origin to a point in the plane with integer coordinates.
This point could be:
(0, 10)
(10, 0)
(0, -10)
(-10, 0)
(6, 8)
(8, 6)
(-6, -8)
(-8, -6)
(6, -8)
(-6, 8)
(-8, 6)
(8, -6)
Once you've drawn any of these lines, there is only one way to draw the square so that it has integer coordinates, so there are 12 possible squares that you can draw.
This point could be:
(0, 10)
(10, 0)
(0, -10)
(-10, 0)
(6, 8)
(8, 6)
(-6, -8)
(-8, -6)
(6, -8)
(-6, 8)
(-8, 6)
(8, -6)
Once you've drawn any of these lines, there is only one way to draw the square so that it has integer coordinates, so there are 12 possible squares that you can draw.
GMAT/MBA Expert
-
[email protected]
- Elite Legendary Member
- Posts: 10392
- Joined: Sun Jun 23, 2013 6:38 pm
- Location: Palo Alto, CA
- Thanked: 2867 times
- Followed by:511 members
- GMAT Score:800
Hi sukhman,
There's a thorough discussion of this question (along with some diagrams) here:
https://www.beatthegmat.com/hard-mgmat-7 ... t9944.html
GMAT assassins aren't born, they're made,
Rich
There's a thorough discussion of this question (along with some diagrams) here:
https://www.beatthegmat.com/hard-mgmat-7 ... t9944.html
GMAT assassins aren't born, they're made,
Rich
GMAT/MBA Expert
-
Brent@GMATPrepNow
- GMAT Instructor
- Posts: 16207
- Joined: Mon Dec 08, 2008 6:26 pm
- Location: Vancouver, BC
- Thanked: 5254 times
- Followed by:1268 members
- GMAT Score:770
Since the square's area is 100, each side must have length 10.A certain square is to be drawn on a coordinate plane. One of the vertices must be on the origin, and the square is to have an area of 100. If all coordinates of the vertices must be integers, how many different ways can this square be drawn?
A. 4
B. 6
C. 8
D. 10
E. 12
If all coordinates of the vertices must be integers, we might immediately see that these 4 squares all meet the given conditions:
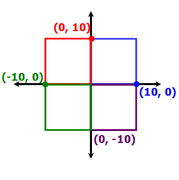
Any others?
You bet.
At this point, we're looking for something called Pythagorean Triplets. These are sets of three INTEGER values that could be the 3 sides of a right triangle.
The two most common ones to remember for the GMAT are 3-4-5 and 5-12-13.
We should also look out for MULTIPLES of these, such as 6-8-10 and 50-120-130
For this question, the 6-8-10 triplet comes into play. So, the hypotenuse (with length 10) will be one side of the square and the 6 and 8 will be the coordinated of the vertex.
Here are 2 such squares in Quadrant I:
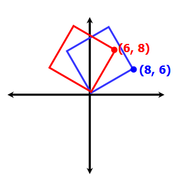
As you might guess, there will be 2 of these types of squares possible in each of the 4 quadrants for a total of 8 squares.
So, the TOTAL number of squares = 4 + 8 = 12
Cheers,
Brent
Brent Hanneson - Creator of GMATPrepNow.com
