(1) (x/|x|) < x
(2) |x| > x
This is Greek to me.
I often find that Absolute Value problems (particularly DS) can get some help through number lines. So first we want to rephrase the stem:mdavidm_531 wrote:If x is not equal to 0, is |x| less than 1?
(1) (x/|x|) < x
(2) |x| > x
This is Greek to me.



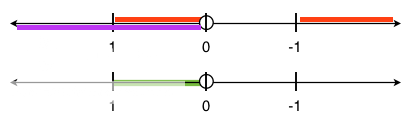
I Think the Numbers are interchanged.. -1 should be in place of 1 because u are drawing number range of X. Correct me if i'm wrongWhitney Garner wrote:I often find that Absolute Value problems (particularly DS) can get some help through number lines. So first we want to rephrase the stem:mdavidm_531 wrote:If x is not equal to 0, is |x| less than 1?
(1) (x/|x|) < x
(2) |x| > x
This is Greek to me.
if x/=0, then is |x|<1?
Using a number line, you can visualize the numbers that make this absolute value expression true? Stuff less than one, BUT also bigger than -1. The new question becomes, "Is x in the shaded region of the number line?"
Statement (1): (x/|x|) < x
If I divide X by the absolute value of X, the X parts of the numbers cancel each other out, and I'm only left to deal with the sign. That means the following:
If x>0, then the left side is positive 1, and if x<0, the left side is negative 1. I have to combine that with the X on the other side:
x>0 ---> 1 < x --> x is either a positive number greater than 1
x<0 ---> -1 < x --> or x is a negative number greater than -1 (between -1 and 0)
If x is a negative number, the answer to our stem is YES, but if x is a positive number our answer is NO. We have shaded parts of the number line BOTH inside and outside of the range we want so the statement is INSUFF
Statement (2): |x| > x
For |x| to be greater than x, it must be the case that x is a negative number so that taking the absolute value makes it positive. If x were positive, then |x| would have to equal x. So our number line for statement (2) becomes:
Because the shaded area is both inside and outside of the range we want - INSUFF.
Statement (1+2):
When we combine the 2 graphs, we shade ONLY the areas included in both statements.
This means that we can only shade an area that is completely included in the desired region - the answer is SUFF.
I like using visuals whenever possible because it can really help clean up scratch paper (and help prevent you making careless errors in long strings of equations/expressions).
Whit