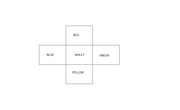
Total number of ways to paint the cube = (total number of ways to arrange the 6 colors)/(total number of ways to orient the cube).abhi332 wrote:You have a six-sided cube and six cans of paint, each a different color. You may not mix colors of paint. How
many distinct ways can you paint the cube using a different color for each side? (If you can reorient a cube to
look like another cube, then the two cubes are not distinct.)
(A) 24
(B) 30
(C) 48
(D) 60
(E) 120
[spoiler]OA:B[/spoiler]
Total number of ways to arrange the 6 colors = 6! = 720.
Total number of ways to orient the cube = 24.
Total number of ways to paint the cube = 720/24 = 30.
The correct answer is B.
Here is one way to count the number of ways that each arrangement can be oriented:
Let say that the 6 colors are A, B, C, D, E and F and that the cube has been painted so that A and B are on opposite faces.
The cube can be oriented so that any of the 6 colors is on top.
Number of options for the color on the top face = 6.
Let's say that the cube has been oriented so that A is on top.
Since A and B are on opposite faces, B is on the bottom.
The cube can now be rotated clockwise so that either C, D, E or F is facing forward.
Number of options for the forward face = 4.
To combine the number of options for the top face and the number of options for the forward face, we multiply:
6*4 = 24.