Problem Solving

Hi, Please find the below problem and suggest me what level it can be ..I feel this is at 650-700..

I got the answer right by adding all the values of squares from 1 - 9...Can you please suggest me if there is an more efficient way of doing this problem.

Hi,

(There is no need to rehash the approach as what Rich has mentioned is perfect)

There is a small formula which is beneficial if you can retain

Sum of squares of n consecutive integers starting from 1 = (1/6) n (n+1) (2n+1)

i.e.
1^2 + 2^2 + 3^2 + .....+ 9^2 = (1/6) 9 (9+1) (2x9+1) = 9 x 10 x 19 / 6 = 285

For a display, identical cubic boxes are stacked in square layers. Each layer consists of cubic boxes arranged in rows that form a square, and each layer has 1 fewer row and 1 fewer box in each remaining row than the layer directly below it. If the bottom of the layer has 81 boxes and the top of the layer has only 1 box, how many boxes are in display?

A. 236
B. 260
C. 269
D. 276
E. 285

The 81 cubes that form the bottom layer look as follows:


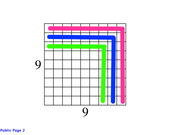
The next layer is formed by removing one entire row, along with one box from each of the remaining rows.
This is the equivalent of removing the pink shaded region in the figure above.
The result is the following figure:

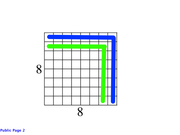
In this layer, the number of cubes = 8² = 64.

To form the next layer, we must remove the blue shaded region.
The result in the following figure:

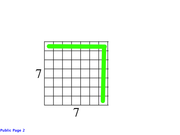
In this layer, the number of cubes = 7² = 49.

By now we should see the pattern.
81, 64 and 49 are consecutive PERFECT SQUARES.
Implication:
The total number of cubes is equal to the sum of the perfect squares between 81 and 1, inclusive:
81+64+49+36+25+16+9+4+1.

The answer choices imply that the sum above must have a units digit of 6, 0, 9 or 5.
Adding together the units digits for the sum above, we get:
(1+4) + (9+6) + (5+6+9) + (4+1) = 5 + 15 + 20 + 5 = 45.
The correct answer choice must have a units digit of 5.

The correct answer is E.