A project requires a rectangular sheet of cardboard satisfying the following requirement: When the sheet is cut into identical rectangular halves, each of the resulting rectangles has the same ratio of length to width as the original sheet. Which of the following sheets comes closest to satisfying the requirement?
(A) A sheet measuring 7 inches by 10 inches
(B) A sheet measuring 8 inches by 14 inches
(C) A sheet measuring 10 inches by 13 inches
(D) A sheet measuring 3 feet by 5 feet
(E) A sheet measuring 5 feet by 8 feet
PS - rectangles
This topic has expert replies
- GMATGuruNY
- GMAT Instructor
- Posts: 15539
- Joined: Tue May 25, 2010 12:04 pm
- Location: New York, NY
- Thanked: 13060 times
- Followed by:1906 members
- GMAT Score:790
When the original sheet is cut into identical halves, each of the resulting rectangles has the same ratio of length to width as the original sheet.abhasjha wrote:A project requires a rectangular sheet of cardboard satisfying the following requirement: When the sheet is cut into identical rectangular halves, each of the resulting rectangles has the same ratio of length to width as the original sheet. Which of the following sheets comes closest to satisfying the requirement?
(A) A sheet measuring 7 inches by 10 inches
(B) A sheet measuring 8 inches by 14 inches
(C) A sheet measuring 10 inches by 13 inches
(D) A sheet measuring 3 feet by 5 feet
(E) A sheet measuring 5 feet by 8 feet
This is possible only if the LENGTH of the original sheet is reduced by half, while the original width STAY THE SAME.
We can PLUG IN THE ANSWERS, which represent the dimensions of the original sheet.
To compare the original ratio to the new ratio, CROSS-MULTIPLY.
Answer choice A:
(original width)/(original length) = 7/10.
New ratio = (1/2 the original length)/(original width) = 5/7.
Setting the ratios equal to each other and cross-multiplying, we get:
7/10 = 5/7
7*7 = 10*5
49 = 50.
Looks good.
Answer choice B:
(original width)/(original length) = 8/14.
New ratio = (1/2 the original length)/(original width) = 7/8.
Setting the ratios equal to each other and cross-multiplying, we get:
8/14 = 7/8
8*8 = 14*7
64 = 98.
Since the resulting values in A are closer to each other, eliminate B.
Answer choice C:
(original width)/(original length) = 10/13.
New ratio = (1/2 the original length)/(original width) = 6.5/10 = 13/20.
Setting the ratios equal to each other and cross-multiplying, we get:
10/13 = 13/20
20*10 = 13*13
200 = 169.
Since the resulting values in A are closer to each other, eliminate C.
Answer choice D:
(original width)/(original length) = 3/5.
New ratio = (1/2 the original length)/(original width) = 2.5/3 = 5/6.
Setting the ratios equal to each other and cross-multiplying, we get:
3/5 = 5/6
6*3 = 5*5
18 = 25.
Since the resulting values in A are closer to each other, eliminate D.
Answer choice E:
(original width)/(original length) = 5/8.
New ratio = (1/2 the original length)/(original width) = 4/5.
5/8 = 4/5
5*5 = 8*4
25 = 32.
Since the resulting values in A are closer to each other, eliminate E.
The correct answer is A.
Private tutor exclusively for the GMAT and GRE, with over 20 years of experience.
Followed here and elsewhere by over 1900 test-takers.
I have worked with students based in the US, Australia, Taiwan, China, Tajikistan, Kuwait, Saudi Arabia -- a long list of countries.
My students have been admitted to HBS, CBS, Tuck, Yale, Stern, Fuqua -- a long list of top programs.
As a tutor, I don't simply teach you how I would approach problems.
I unlock the best way for YOU to solve problems.
For more information, please email me (Mitch Hunt) at [email protected].
Student Review #1
Student Review #2
Student Review #3
Followed here and elsewhere by over 1900 test-takers.
I have worked with students based in the US, Australia, Taiwan, China, Tajikistan, Kuwait, Saudi Arabia -- a long list of countries.
My students have been admitted to HBS, CBS, Tuck, Yale, Stern, Fuqua -- a long list of top programs.
As a tutor, I don't simply teach you how I would approach problems.
I unlock the best way for YOU to solve problems.
For more information, please email me (Mitch Hunt) at [email protected].
Student Review #1
Student Review #2
Student Review #3
GMAT/MBA Expert
- [email protected]
- Elite Legendary Member
- Posts: 10392
- Joined: Sun Jun 23, 2013 6:38 pm
- Location: Palo Alto, CA
- Thanked: 2867 times
- Followed by:511 members
- GMAT Score:800
Hi abhasjha,
This question has a couple of great pattern-matcher's shortcuts built into it.
First, when cutting a rectangle in half (as the question describes), the only possible way for the ratio of sides to be close is if you cut the LONG SIDE in half. Here's why, using Answer A as an example...
If we start with a 7 x 10 sheet and cut the 7 "in half", then we end up with...
3.5 x 10 which is NOT close to the original ratio (it's half of the original ratio. Cutting the 10 "in half" gives us...
7 x 5 which we can "flip around" (since either dimension can the length or the width). This gives us a close ratio...
7 x 10 vs. 5 x 7
Second, knowing fraction-to-decimal conversions makes the math a little easier....
7/10 = .7
5/7 = about .71
While I would check the other answers just to be sure, I can't imagine that any of the ratios would be closer than this.
GMAT assassins aren't born, they're made,
Rich
This question has a couple of great pattern-matcher's shortcuts built into it.
First, when cutting a rectangle in half (as the question describes), the only possible way for the ratio of sides to be close is if you cut the LONG SIDE in half. Here's why, using Answer A as an example...
If we start with a 7 x 10 sheet and cut the 7 "in half", then we end up with...
3.5 x 10 which is NOT close to the original ratio (it's half of the original ratio. Cutting the 10 "in half" gives us...
7 x 5 which we can "flip around" (since either dimension can the length or the width). This gives us a close ratio...
7 x 10 vs. 5 x 7
Second, knowing fraction-to-decimal conversions makes the math a little easier....
7/10 = .7
5/7 = about .71
While I would check the other answers just to be sure, I can't imagine that any of the ratios would be closer than this.
GMAT assassins aren't born, they're made,
Rich
GMAT/MBA Expert
- Brent@GMATPrepNow
- GMAT Instructor
- Posts: 16207
- Joined: Mon Dec 08, 2008 6:26 pm
- Location: Vancouver, BC
- Thanked: 5254 times
- Followed by:1268 members
- GMAT Score:770
Here's an algebraic solution:abhasjha wrote:A project requires a rectangular sheet of cardboard satisfying the following requirement: When the sheet is cut into identical rectangular halves, each of the resulting rectangles has the same ratio of length to width as the original sheet. Which of the following sheets comes closest to satisfying the requirement?
(A) A sheet measuring 7 inches by 10 inches
(B) A sheet measuring 8 inches by 14 inches
(C) A sheet measuring 10 inches by 13 inches
(D) A sheet measuring 3 feet by 5 feet
(E) A sheet measuring 5 feet by 8 feet
Let x be length of the LONG side of the original rectangle
Let y be length of the SHORT side of the original rectangle
Then cut the rectangle into two pieces
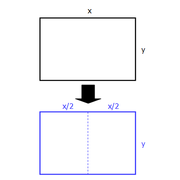
We want the resulting rectangles to have the same ratio of length to width as the original sheet.
In other words, we want x/y = y/(x/2)
Cross multiply to get: x²/2 = y²
Multiply both sides by 2 to get: x² = 2y²
Divide both sides by y² to get: x²/y² = 2
Take square root of both sides to get: x/y = √2
IMPORTANT: For the GMAT, everyone should know the following APPROXIMATIONS: √2 ≈ 1.4, √3 ≈ 1.7, √5 ≈ 2.2
So, we know that x/y ≈ 1.4
In other words, the ratio (LONG side)/(SHORT side) ≈ 1.4
Now check the answer choices:
(A) 10/7 = 1 3/7 ≈ 1.4 LOOKS GOOD!
(B) 14/8 = 1 6/8 = 1.75 ELIMINATE
(C) 13/10 = 1.3 ELIMINATE
(D) 5/3 = 1 2/3 ≈ 1.66 ELIMINATE
(E) 8/5 = 1.6 ELIMINATE
Answer: A
Cheers,
Brent
Last edited by Brent@GMATPrepNow on Thu Apr 19, 2018 1:38 pm, edited 1 time in total.
Can you elaborate more on this statement? For example, w=8, L=14 so 8/14 to 8/7, why we flip 8/7 to 7/8?This is possible only if the LENGTH of the original sheet is reduced by half, while the original width STAY THE SAME.
it should be
Original W/original L compared with New W/new L?





















