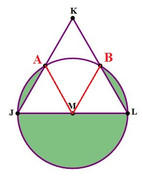
Mike@Magoosh wrote:
In the diagram above, JKL is an equilateral triangle. Point M is the midpoint of segment JL, and M is the center of a circle that passes through points J and L. The shaded regions in the diagram indicate all the regions inside the circle that are outside the triangle. What fraction of the total area of the circle is outside the triangle?
(A) 2/(pi)
(B) [(pi) - sqrt(3)]/(pi)
(C) [4 - sqrt(3)]/(pi)
(D) (2/3) - [sqrt(3)/(4pi)]
(E) (5/6) - [sqrt(3)/(2pi)]
Alternate approach:
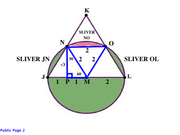
Let r=2.
Area of the circle = πr² = π(2²) = 4π.
Outside trapezoid JNOL are 3 slivers, moving clockwise from point J:
Green sliver JN, red sliver NO, and green sliver OL.
Sum of the 3 slivers = (1/2 circle) - (trapezoid JNOL)
1/2 of the circle = (1/2)(4Ï€) = 2Ï€
Area of JNOL = (b� + b₂)/2 * h = (JL + NO)/2 * NP = (4 + 2)/2 * √3 = 3√3.
Thus:
Sum of the 3 slivers = 2π - 3√3.
Since green slivers JN and OL constitute only 2 of the 3 slivers, we get:
Sliver JN + Sliver OL = (2/3)(2π - 3√3) = (4π - 6√3)/3.
Adding the green semicircle to green slivers JN and OL, we get the entire green portion:
2π + (4π - 6√3)/3 = (6π + 4π - 6√3)/3 = (10π - 6√3)/3.
Thus:
(total green portion)/(total circle) = [ (10π - 6√3)/3 ] / 4π = (10π - 6√3)/12π = 5/6 - √3/(2π).
The correct answer is
E.
Last edited by
GMATGuruNY on Tue Jul 15, 2014 10:36 am, edited 1 time in total.
Private tutor exclusively for the GMAT and GRE, with over 20 years of experience.
Followed here and elsewhere by over 1900 test-takers.
I have worked with students based in the US, Australia, Taiwan, China, Tajikistan, Kuwait, Saudi Arabia -- a long list of countries.
My students have been admitted to HBS, CBS, Tuck, Yale, Stern, Fuqua -- a long list of top programs.
As a tutor, I don't simply teach you how I would approach problems.
I unlock the best way for YOU to solve problems.
For more information, please email me (Mitch Hunt) at
[email protected].
Student Review #1
Student Review #2
Student Review #3
