If a 30%-solution of alcohol was mixed with a 50%-solution of alcohol to obtain 10 liters of a 45%-solution of alcohol, how much of the 30%-solution was used?
A. 2.0 liters
B. 2.5 liters
C. 2.7 liters
D. 3.0 liters
E. 3.2 liters
OA : B
If a 30%-solution of alcohol was mixed with
This topic has expert replies
- DavidG@VeritasPrep
- Legendary Member
- Posts: 2663
- Joined: Wed Jan 14, 2015 8:25 am
- Location: Boston, MA
- Thanked: 1153 times
- Followed by:128 members
- GMAT Score:770
If we plot the solution percentages on a number line, we'll get:NandishSS wrote:If a 30%-solution of alcohol was mixed with a 50%-solution of alcohol to obtain 10 liters of a 45%-solution of alcohol, how much of the 30%-solution was used?
A. 2.0 liters
B. 2.5 liters
C. 2.7 liters
D. 3.0 liters
E. 3.2 liters
OA : B
30----------------45-----50
Gap:------15--------5------
Notice that we have a 15:5 or 3:1 ratio of the two components, so we can call them 3x and x. Notice also that we must have more of the 50% solution than the 30% solution as the overall average is closer to 50%.
50% solution: 3x
30% solution: x
Total: 10
3x + x = 10 ---> 4x = 10 ---> x = 2.5. The answer is B.
GMAT/MBA Expert
- Brent@GMATPrepNow
- GMAT Instructor
- Posts: 16207
- Joined: Mon Dec 08, 2008 6:26 pm
- Location: Vancouver, BC
- Thanked: 5254 times
- Followed by:1268 members
- GMAT Score:770
Let's keep track of the volume of pure alcoholNandishSS wrote:If a 30%-solution of alcohol was mixed with a 50%-solution of alcohol to obtain 10 liters of a 45%-solution of alcohol, how much of the 30%-solution was used?
A. 2.0 liters
B. 2.5 liters
C. 2.7 liters
D. 3.0 liters
E. 3.2 liters
The combined solution has a volume of 10 liters, and it's 45% pure alcohol
45% of 10 liters = (0.45)(10) = 4.5 liters
So, the combined solutions contains 4.5 liters of PURE alcohol
Let x = the volume of 30% solution
So, 10-x = the volume of 50% solution (since we have 10 liters of resulting combined solution
This means 0.3x = the volume of PURE alcohol in the 30% solution
And 0.5(10 - x) = the volume of PURE alcohol in the 50% solution
We can write: 0.3x + 0.5(10 - x) = 4.5
Expand: 0.3 + 5 - 0.5x = 4.5
Simplify: 5 - 0.2x = 4.5
Subtract 5 from both sides: -0.2x = -0.5
Divide both sides by -0.2 to get: x = 2.5
Answer: B
Cheers,
Brent
GMAT/MBA Expert
- ErikaPrepScholar
- Legendary Member
- Posts: 503
- Joined: Thu Jul 20, 2017 9:03 am
- Thanked: 86 times
- Followed by:15 members
- GMAT Score:770
Right off the bat, the word "mixed" should indicate that this is a mixture problem. This means that we'll be setting up equations using what we know from the problem.
The problem tells us that we combine some amount of a 30% alcohol solution with some amount of a 50% alcohol solution. This gives us 10 liters of a 45% alcohol solution. Let's say we have X liters of 30% alcohol solution and Y liters of 50% alcohol solution. We want to solve for X. We can build one equation for the total volume of the solution:
X + Y = 10
and one equation for the total alcohol content of the solution:
0.3X + 0.5Y = 0.45 (X+Y)
Simplifying gives:
0.3X + 0.5Y = 0.45X + 0.45Y
0.05Y = 0.15X
Y = 3X
Plugging that into our initial equation gives:
X + 3X = 10
4X = 10
X = 10/4
X = 2.5
Or answer choice B.
Alternatively, you can solve by visualizing where the percents fall on a number line.
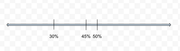
50% is 3 times closer to 45% than 30% is. This means there must be 3 times as much of the 50% solution in the final solution than there is of the 30% solution. So Y = 3X. Knowing that X + Y = 10, we can solve for X using the math shown above.
The problem tells us that we combine some amount of a 30% alcohol solution with some amount of a 50% alcohol solution. This gives us 10 liters of a 45% alcohol solution. Let's say we have X liters of 30% alcohol solution and Y liters of 50% alcohol solution. We want to solve for X. We can build one equation for the total volume of the solution:
X + Y = 10
and one equation for the total alcohol content of the solution:
0.3X + 0.5Y = 0.45 (X+Y)
Simplifying gives:
0.3X + 0.5Y = 0.45X + 0.45Y
0.05Y = 0.15X
Y = 3X
Plugging that into our initial equation gives:
X + 3X = 10
4X = 10
X = 10/4
X = 2.5
Or answer choice B.
Alternatively, you can solve by visualizing where the percents fall on a number line.

50% is 3 times closer to 45% than 30% is. This means there must be 3 times as much of the 50% solution in the final solution than there is of the 30% solution. So Y = 3X. Knowing that X + Y = 10, we can solve for X using the math shown above.

Erika John - Content Manager/Lead Instructor
https://gmat.prepscholar.com/gmat/s/
Get tutoring from me or another PrepScholar GMAT expert: https://gmat.prepscholar.com/gmat/s/tutoring/
Learn about our exclusive savings for BTG members (up to 25% off) and our 5 day free trial
Check out our PrepScholar GMAT YouTube channel, and read our expert guides on the PrepScholar GMAT blog
- GMATGuruNY
- GMAT Instructor
- Posts: 15539
- Joined: Tue May 25, 2010 12:04 pm
- Location: New York, NY
- Thanked: 13060 times
- Followed by:1906 members
- GMAT Score:790
An alternate approach is to PLUG IN THE ANSWERS, which represent the amount of 30% solution.NandishSS wrote:If a 30%-solution of alcohol was mixed with a 50%-solution of alcohol to obtain 10 liters of a 45%-solution of alcohol, how much of the 30%-solution was used?
A. 2.0 liters
B. 2.5 liters
C. 2.7 liters
D. 3.0 liters
E. 3.2 liters
When the correct answer is plugged in, the average alcohol percentage per 10 liters = 45%.
D: 3 liters 30% solution, implying 7 liters 50% solution
Average alcohol percentage per 10 liters = (3*30 + 7*50)/10 = (90+350)/10 = 440/10 = 44%.
The resulting alcohol percentage is TOO LOW.
To increase the resulting alcohol percentage, we must use MORE 50% SOLUTION (since it has a higher percentage of alcohol) and LESS 30% SOLUTION (since it has a lower percentage of alcohol).
Eliminate D and E.
B: 2.5 liters 30% solution, implying 7.5 liters 50% solution
Average alcohol percentage per 10 liters = (2.5*30 + 7.5*50)/10 = (75 + 375)/10 = 450/10 = 45%.
Success!
The correct answer is B.
Private tutor exclusively for the GMAT and GRE, with over 20 years of experience.
Followed here and elsewhere by over 1900 test-takers.
I have worked with students based in the US, Australia, Taiwan, China, Tajikistan, Kuwait, Saudi Arabia -- a long list of countries.
My students have been admitted to HBS, CBS, Tuck, Yale, Stern, Fuqua -- a long list of top programs.
As a tutor, I don't simply teach you how I would approach problems.
I unlock the best way for YOU to solve problems.
For more information, please email me (Mitch Hunt) at [email protected].
Student Review #1
Student Review #2
Student Review #3
Followed here and elsewhere by over 1900 test-takers.
I have worked with students based in the US, Australia, Taiwan, China, Tajikistan, Kuwait, Saudi Arabia -- a long list of countries.
My students have been admitted to HBS, CBS, Tuck, Yale, Stern, Fuqua -- a long list of top programs.
As a tutor, I don't simply teach you how I would approach problems.
I unlock the best way for YOU to solve problems.
For more information, please email me (Mitch Hunt) at [email protected].
Student Review #1
Student Review #2
Student Review #3
If a 30%-solution of alcohol was mixed with a 50%-solution of alcohol to obtain 10 liters of a 45%-solution of alcohol, how much of the 30%-solution was used?
A. 2.0 liters
B. 2.5 liters
C. 2.7 liters
D. 3.0 liters
E. 3.2 liters
Solution:
Let 30%-solution of alcohol be 'x' litres.
Then 50%-solution of alcohol will be '(10-x)' litres.
The situation described in the problem statement can be described in equation form as,
'x' litres of 30%-solution + '(10-x)' litres of 50%-solution = 10 litres of 45%-solution
x(30%) + (10 - x)(50%) = 10(45%)
Converting percentages to decimals
x (30/100) +(10-x)(50/100) = 10(45/100)
Simplifying
0.3x + 0.5(10 - x) = 10(0.45)
Using Distributive Property
0.3x + 5 - 0.5x = 4.5
Combining like terms
0.3x -0.5x = 4.5 - 5
Simplifying
-0.2x = -0.5
0.2x = 0.5
x = 0.5/0.2
x = 2.5 litres
Hence, 2.5 litres of 30%-solution was used.
Option B is the correct answer.
A. 2.0 liters
B. 2.5 liters
C. 2.7 liters
D. 3.0 liters
E. 3.2 liters
Solution:
Let 30%-solution of alcohol be 'x' litres.
Then 50%-solution of alcohol will be '(10-x)' litres.
The situation described in the problem statement can be described in equation form as,
'x' litres of 30%-solution + '(10-x)' litres of 50%-solution = 10 litres of 45%-solution
x(30%) + (10 - x)(50%) = 10(45%)
Converting percentages to decimals
x (30/100) +(10-x)(50/100) = 10(45/100)
Simplifying
0.3x + 0.5(10 - x) = 10(0.45)
Using Distributive Property
0.3x + 5 - 0.5x = 4.5
Combining like terms
0.3x -0.5x = 4.5 - 5
Simplifying
-0.2x = -0.5
0.2x = 0.5
x = 0.5/0.2
x = 2.5 litres
Hence, 2.5 litres of 30%-solution was used.
Option B is the correct answer.
GMAT/MBA Expert
- Scott@TargetTestPrep
- GMAT Instructor
- Posts: 7264
- Joined: Sat Apr 25, 2015 10:56 am
- Location: Los Angeles, CA
- Thanked: 43 times
- Followed by:29 members
We can let x = the amount of 30% solution and y = the amount of 50% solution. Thus:NandishSS wrote:If a 30%-solution of alcohol was mixed with a 50%-solution of alcohol to obtain 10 liters of a 45%-solution of alcohol, how much of the 30%-solution was used?
A. 2.0 liters
B. 2.5 liters
C. 2.7 liters
D. 3.0 liters
E. 3.2 liters
OA : B
x + y = 10
y = 10 - x
and
0.3x + 0.5y = 0.45(x + y)
30x + 50y = 45x + 45y
5y = 15x
y = 3x
Substituting 3x for y in y = 10 - x, we have:
3x = 10 - x
4x = 10
x = 10/4 = 2.5
Alternate Solution:
We mix x liters of 30% solution with (10 - x) liters of 50% solution to obtain 10 liters of 45% solution. We can express this information in the following equation:
x(0.30) + (10 - x)(0.50) = 10(0.45)
0.3x + 5 - 0.5x = 4.5
3x + 50 - 5x = 45
-2x = -5
x = 5/2, or 2.5
Answer: B
Scott Woodbury-Stewart
Founder and CEO
[email protected]

See why Target Test Prep is rated 5 out of 5 stars on BEAT the GMAT. Read our reviews






















