If each line segment in the figure is equal to 4, we're looking for the area of 3 equal RHOMBUSES (rhombi? No one knows).

(Forgive the crude rendering... geometry is always the hardest to explain digitally!)



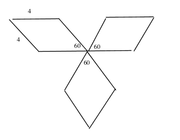
If the angles a, b, and c are all 60, then the opposite angles are 60, and the other angles 120:



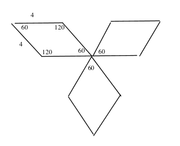
This means that we can chop each rhombus into 2 identical EQUILATERAL triangles. (Btw, the 60-120-60-120 rhombus is the most common form of a rhombus on the GMAT).



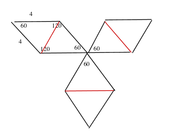
Now, we can simply calculate the area of a single equilateral triangle, then multiply by 6.

AREA OF EQUILATERAL: remember that you can chop an equilateral triangle into two 30-60-90 right triangles. You should have the ratio for these memorized:



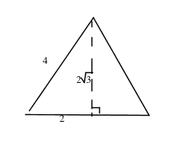
Thus, the base of each triangle is 4, and the height is 2(sqrt3). So (1/2)bh = 4(sqrt3)

Since we have 6 such equilateral triangles, the total area = (6)(4(sqrt3)) = 24(sqrt3)

The answer is E.

For a somewhat similar area-of-rhombus question, see example #2 in this article: https://www.manhattanprep.com/gmat/blog ... ncy-wrong/