Problem Solving

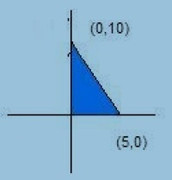
Point (x, y) is a point within the triangle. What is the probability that y < x?

A. 1/4
B. 1/3
C. 1/6
D. 1/2
E. 1/5

The OA is B.

I don't have clear this PS question, I appreciate if any expert explain it for me. Thank you so much.

Hi AAPL,
Lets take a look at your question.

We will first find the equation of the line connecting the two points (0, 10) and (5, 0).
$$Slope\ =\ \frac{0-10}{5-0}=-\frac{10}{5}=-2$$
Equation of line can be written as:
$$y-0=-2\left(x-5\right)$$
$$y=-2x+10$$
Now we will find the points (x,y) using the equation.
For x=0,
y=-2x+10=-2(0)+10=10
$$\left(0,\ 10\right)$$

For x=1,
y=-2x+10=-2(1)+10=8
$$\left(1,\ 8\right)$$

For x=2,
y=-2x+10=-2(2)+10=6
$$\left(2,\ 6\right)$$

For x=3,
y=-2x+10=-2(3)+10=4
$$\left(3,\ 4\right)$$

For x=4,
y=-2x+10=-2(4)+10=2
$$\left(4,\ 2\right)$$

For x=5,
y=-2x+10=-2(5)+10=0
$$\left(5,\ 0\right)$$

We need to find the points where y < x.
We can see only two such points out of the total 6 points we calculated above, i.e. (4, 2) and (5, 0).

Hence P(y < x) can be calculated as,
$$=\frac{2}{6}=\frac{1}{3}$$
Therefore, Option B is correct.

Hope it helps.
I am available if you'd like any follow up.